3.4 The Distribution Function

Figure 3.5: Fermi-Dirac equilibrium distribution function and Maxwell-Boltzmann approximations at 300K and 1000K.

As the solution variable of the Boltzmann transport equation, the distribution function plays an important role for the description of transport within semiconductor devices. The distribution function of electrons and holes in thermal equilibrium is the Fermi-Dirac distribution

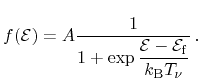$$\ensuremath{f}(\ensuremath{\mathcal{E}}) = A \frac{1}{1+\exp{\dis... ...\mathrm{f}}}}}{k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}}}}} \,.$$ (3.15)

A commonly used approximation to the Fermi-Dirac distribution function is the Maxwell-Boltzmann distribution

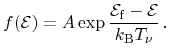$$\ensuremath{f}(\ensuremath{\mathcal{E}}) = A \exp{\frac{\ensurema... ...th{\mathcal{E}}}{k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}}} \,.$$ (3.16)

From a mathematical point of view, the 1 in the denominator of (3.15) can be neglected, if the second term dominates. This is valid if the difference between the carrier's energy and the Fermi level is large compared to 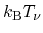$k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}$ , which is the case in non-degenerate semiconductors. While the Fermi-Dirac distribution incorporates Pauli's exclusion principle, which becomes important at high dopings, the Maxwell-Boltzmann distribution neglects this principle. Thus, the Maxwell-Boltzmann distribution's validity is limited to the lowly doped case.

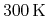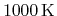Fig. 3.5 illustrates the situation for a semiconductor in equilibrium. Both Fermi-Dirac and Maxwell-Boltzmann statistics are plotted for $300\,\ensuremath{\mathrm{K}}$ and $1000\,\ensuremath{\mathrm{K}}$ , respectively. While the transition at the Fermi level is relatively sharp at lower temperatures, it is extended to a higher energy range at elevated temperatures. For intrinsic and lowly doped semiconductors, the range where the deviation between Fermi-Dirac and Maxwell-Boltzmann statistics accounts for a non-negligible error is completely covered by the forbidden energy gap. However, the Fermi energy is shifted close to the band edge in highly doped samples and thus the range with non-negligible deviations between Maxwell-Boltzmann statistics and Fermi-Dirac statistics reaches energy levels outside the forbidden gap.

While (3.16) represents the equilibrium case, carrier transport can be incorporated by a displaced Maxwellian, which reads assuming parabolic bands (3.13)

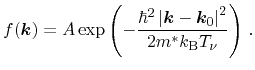$$\ensuremath{f}(\ensuremath{\ensuremath{\mathitbf{k}}}) = A \exp \... ...t^2}{2 m^*k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}} \right) \,.$$ (3.17)

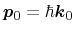Here, $\ensuremath{\ensuremath{\mathitbf{p}}}_0 = \hbar\ensuremath{\ensuremath{\mathitbf{k}}}_0$ is the average momentum of the carriers and their average velocity reads 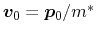$\ensuremath{\ensuremath{\mathitbf{v}}}_0 = \ensuremath{\ensuremath{\mathitbf{p}}}_0/m^*$ . Especially in thermoelectric devices, the deterministic shift of the distribution function is very small compared to the stochastic movement due to non-zero temperature. Therefore, the diffusion approximation can be applied, where the displaced Maxwellian (3.17) is expanded to is Taylor series and truncated after the first-order term [73]

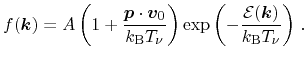$$\ensuremath{f}(\ensuremath{\ensuremath{\mathitbf{k}}}) = A \left(... ...bf{k}}})}{k_\ensuremath{\mathrm{B}}\ensuremath{T_\ensuremath{\nu}}} \right) \,.$$ (3.18)

For the derivation of electrical transport models in the next sections, Maxwell-Boltzmann statistics in the formulation of (3.18) have been assumed for the closure relations due to reasons of mathematical convenience. However, strictly speaking this approximation consequently affects macroscopic quantities, which are assessed in Section 3.5.1.

M. Wagner: Simulation of Thermoelectric Devices