next up previous contents
Next: 6.1.1 Analytical Inductance and Up: 6. Applications Previous: 6. Applications   Contents


6.1 Inductance and Resistance of a Coaxial Structure

The quasi-magnetostatic case from Section 5.2 is well suited for extraction of inductance and resistance of a given structure. Distributed phenomena like proximity and skin effect can also be analyzed. The finite element method on unstructured meshes allows to obtain these parameters in arbitrary regions with complex shape, for which no analytical procedures exist. This section handles intentionally a coaxial structure, for which analytical solutions for the inductance and for the resistance exist. It is interesting to obtain these parameters numerically and compare the results with the analytical calculations, or to evaluate the method from Section 5.2 at least for this special case.

The simulated coaxial structure is shown in Fig. <6.1>. The radius $ r$ of the inner conductor is $ a$ . The outer conductor has an inner radius $ b$ and an outer radius $ c$ . The conductor is assumed with $ \mu_r = 1$ and $ \gamma = 38{\cdot}10^6$ $ [\Omega{}m]^{-1}$ . The dielectric material between the inner and the outer conductor ($ a < r < b$ ) and outside the outer conductor ($ r > c$ ) has $ \mu_r = 1$ and $ \gamma = 10^{-4}$ $ [\Omega{}m]^{-1}$ . On the curve $ \mathcal{C}_{in}$ around the inner conductor the magnetic field $ H_{in}$ is applied. This is managed by applying $ \vec{H}_{in}$ to each edge which belongs to $ \mathcal{C}_{in}$ and causes a current $ I$ in the inner inductor

$\displaystyle I = \int_{\mathcal{C}_{in}}\vec{H}_1 \mathrm{d}\vec{r} = \int_{\... ...}\vec{r} = \int_{\mathcal{C}_{in}}\vec{H} \mathrm{d}\vec{r} = H_{in}\sum_il_i.$ (6.1)

In (6.1) $ l_i$ is the length of the $ i$ -th edge, which belongs to $ \mathcal{C}_{in}$ and the sum applies to all edge lengths building $ \mathcal{C}_{in}$ . Along $ \mathcal{C}_{out}$ (Fig. <6.1>) the magnetic field $ H_{out}$ is set consistently to zero. This requires that the current $ I$ in the inner conductor given by $ H_{in}$ on $ \mathcal{C}_{in}$ flows back in the outer conductor. The resulting current density distribution is shown in Fig. <6.2> by directed cones placed in the nodes of the simulation domain. The size and the darkness of the cones correspond to the magnitude of the current density. Note that the current density in the inner conductor is not equal to the one in the outer one, because of the different cross sections of the conductors. The corresponding magnetic field distribution is similarly illustrated in Fig. <6.3>. It is not difficult to see that the curves $ \mathcal{C}_{in}$ and $ \mathcal{C}_{out}$ represent the Dirichlet boundary for $ \vec{H}_1$ . The magnetic field on the edges which belong to $ \mathcal{C}_{in}$ is $ H_i$ and zero on $ \mathcal{C}_{out}$ , respectively. For the $ \psi$ field it is sufficient that a value of $ \psi$ is given on one node of the simulation domain. Since the gradient of $ \psi$ is determining and not $ \psi$ itself, this value can be chosen arbitrarily.

Such a coaxial structure is well suited for the comparison between simulation and analytical results, because analytical formulas can be given. Just homogeneous Neumann boundary conditions (5.30) and (5.32) are exactly satisfied also for finite dimensions (Refer to Fig. <6.3>). The field $ \vec{H}$ has no normal component to the outer surface of the simulation domain. For isotropic materials in terms of the relative permeability $ \mu_r$ the magnetic flux $ \vec{B}$ will have the same direction as $ \vec{H}$ and the Neumann boundary condition (5.30) is satisfied independently of the size of the simulation domain. Analogously the same can be considered for the electric field $ \vec{E}$ . Related to the electric conductivity $ \gamma$ the materials in the simulation domain are assumed isotropic. Because of the finite conductivity $ \gamma$ in the conducting parts the corresponding electric field $ \vec{E}$ cannot be neglected. This is the reason why the dielectric layer (its thickness can be chosen arbitrarily) outside of the outer conductor is used. For the outer boundary, which lies on the dielectric, $ \vec{E}$ is zero. For the remaining part of the outer boundary the current density distribution $ \vec{J }$ is normal to the outer faces of the conducting regions, as demonstrated in Fig. <6.2>.

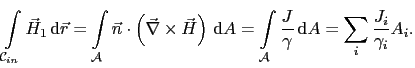$\displaystyle \int_{\mathcal{C}_{in}}\vec{H}_1 \mathrm{d}\vec{r} = \int_\mathc... ... \int_\mathcal{A}\frac{J}{\gamma} \mathrm{d}A = \sum_i\frac{J_i}{\gamma_i}A_i.$ (6.2)

$ \mathcal{A}$ is the outer face enclosed from $ \mathcal{C}_{in}$ and $ A_i$ is the $ i$ -th area of the triangular elements, in which this face is discretized. Thus $ \vec{E}$ is either zero or perpendicular to the outer face and the homogeneous Neumann boundary condition (5.32) is satisfied, also for finite domain size.

Figure 6.1: The simulated coaxial structure.
\includegraphics[width=14cm]{figures/applications/coax/coax_mark.eps}

Figure 6.2: Current density distribution.
\includegraphics[width=14cm]{figures/applications/coax/coax_demo_i.eps}

Figure 6.3: Magnetic field.
\includegraphics[width=14cm]{figures/applications/coax/coax_demo_h.eps}


Subsections
next up previous contents
Next: 6.1.1 Analytical Inductance and Up: 6. Applications Previous: 6. Applications   Contents
A. Nentchev: Numerical Analysis and Simulation in Microelectronics by Vector Finite Elements