6.1.2 Numerical Inductance and Resistance Extraction

The electro-magnetic power in the domain $\mathcal{V}$ can be expressed in two different ways. The first one is by volume integration over the power density distribution [103] in the region $\mathcal{V}$ . The second one is by the current flowing trough the resulting resistance and inductance. As aforementioned, the quasi-magnetostatic case is considered

$\displaystyle \int_{\mathcal{V}}\left(\vec{J}\cdot\vec{E} + \vec{H}\cdot\partial_t\vec{B}\right)\mathrm{d}V = LI\frac{dI}{dt} + RI^2.$

(6.13)

In the frequency domain using the constitutive relations (4.7) and (4.8) one obtains

$\displaystyle \int_{\mathcal{V}}\left(\frac{J^2}{\gamma} + \jmath\omega\mu{}H^2\right)\mathrm{d}V = \jmath\omega{}LI^2 + RI^2.$

(6.14)

$\displaystyle P_1 = \int_{\mathcal{V}}\frac{J^2}{\gamma} \mathrm{d}V, P_2 ... ...mega\int_{\mathcal{V}}\mu{}H^2 \mathrm{d}V, \mathrm{and} P = P_1 + P_2.$

(6.15)

Consequently the resistance

and the inductance

arising in the domain $\mathcal{V}$ are calculated by

The domain $\mathcal{V}$ is discretized and the linear equation system (5.37) is assembled as described in Section 5.2 and solved to obtain the solution vector $\{c\}$ . The indexes

of the coefficients

are arranged as shown in Section 5.2. The fields $\vec{H}_1$ and $\psi$ are constructed as in (5.27) and (5.28). $\vec{H}$ is obtained by (5.23). These quantities are used to determine

. Inserting (5.13) in the expression for

from (6.15) gives

$\begin{displaymath}\begin{split}P_1 & = \int_{\mathcal{V}}\frac{1}{\gamma}\left(... ...\nabla}\times\vec{N}_j\right) \right]^2 \mathrm{d}V \end{split}\end{displaymath}$

(6.17)

$\begin{displaymath}\begin{split}P_1 & = \sum_{i=1}^m c_i \sum_{j=1}^m \int_{\m... ...vec{\nabla}\times\vec{N}_j\right) \mathrm{d}V c_j. \end{split}\end{displaymath}$

(6.18)

$\displaystyle P_2 = \jmath\omega\int_{\mathcal{V}}\mu \left( \sum_{j=1}^{m}c_j\... ...la}\lambda_j - \sum_{j=M+1}^{N}c_j\vec{\nabla}\lambda_j \right)^2 \mathrm{d}V,$

(6.20)

$\begin{displaymath}\begin{split}\frac{P_2}{\jmath\omega} & = \left.\sum_ic_i\sum... ... [m+1;n]\cup[M+1;N], j \in [m+1;n]\cup[M+1;N]}. \end{split}\end{displaymath}$

(6.21)

Using (6.18) and (6.21) for

and

the very suitable form for the power

in the simulation domain is derived

$\displaystyle P = P_1 + P_2 = \left\{c\right\}^T \left[\begin{array}{llll} A_1 ... ...2 & A_3 & B_3 B_2^T & C_2 & B_3^T & C_3 \end{array}\right] \left\{c\right\},$

(6.22)

where the sub-matrices

and

with $k\in[1;3]$ are calculated using the mathematical expressions given in (5.38), (5.39), and (5.40), respectively. The indexes

and

indicate the different ranges of the sub-matrix entries global indexes

and

. The associated global index ranges are specified in (6.18) and (6.21) and can be given more clearly as follows:

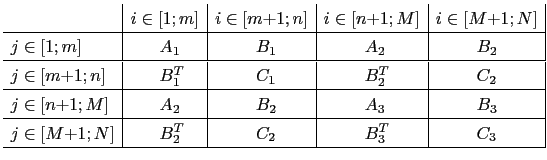$\displaystyle \renewedcommand{arraystretch}{1.3} \begin{array}{l\vert l\vert l\... ... C_2 & B_3^T & C_3 \hline \end{array}$

In (5.37) only the $n\times{}n$ part of the matrix for the unknowns is used. The remaining part is assembled with the known Dirichlet values directly to right hand side vector $\{b\}$ . For the power calculation (6.22) the whole $N\times{}N$ matrix is used. Expression (6.22) can be simplified by involving (5.37)

$\displaystyle P = \left\{c_{n+1} ... c_N\right\} \begin{array}{\vert llll\ver... ..._2 & B_2 & A_3 & B_3 B_2^T & C_2 & B_3^T & C_3 \end{array} \left\{c\right\}.$

(6.23)

**Figure 6.4:** Current density distribution at low frequency.
$\includegraphics[width=7cm]{figures/applications/coax/coax_i_f3e7_scaled.eps}$

**Figure 6.5:** Current density distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_i_f3e10_scaled.eps}$

**Figure 6.6:** Current density distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_i_f3e11_scaled.eps}$

**Figure 6.7:** Current density distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_i_f3e12_scaled.eps}$

**Figure 6.8:** Magnetic field distribution at low frequency.
$\includegraphics[width=7cm]{figures/applications/coax/coax_h_f3e7_scaled.eps}$

**Figure 6.9:** Magnetic field distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_h_f3e10_scaled.eps}$

**Figure 6.10:** Magnetic field distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_h_f3e11_scaled.eps}$

**Figure 6.11:** Magnetic field distribution at GHz.
$\includegraphics[width=7cm]{figures/applications/coax/coax_h_f3e12_scaled.eps}$