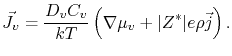2.3 Electromigration Induced Material Transport

Although electromigration refers to the transport of material caused by the momentum transfer from conducting electrons to metal atoms [1], the total atomic migration is influenced by other physical mechanisms. Electromigration constitutes a diffusion-convection problem, where atomic transport along the interconnect line occurs due to a combination of several driving forces. Since the atomic migration occurs via a vacancy exchange mechanism, the material transport can be, in general, described in terms of vacancies as

$$\vec\JV = \frac{\DV\CV}{\kB\T}\left( \ensuremath{\nabla{\symVacChemPot}} + \vert\Z\vert \ee\symElecRes\vec\symCurrDens \right).$$ (2.11)

$\vec\JV$ is the vacancy flux, $\DV$ is the vacancy diffusivity, $\CV$ is the vacancy concentration, and $\symVacChemPot$ is the chemical potential of vacancies.

In sites of flux divergence vacancies can accumulate or vanish depending on the sign of the divergence, and the material balance is given by the usual continuity equation

$$\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}} = -\ensuremath{\nabla\cdot{\vec\JV}} + \G,$$ (2.12)

where $\G$ represents a generation or annihilation term.

Equations (2.11) and (2.12) are the basic continuum equations which describe the total mass transport along an interconnect line due to electromigration and accompanying driving forces.

The model proposed by Shatzkes and Lloyd [50] was the first that rigorously derived the interconnect lifetime with an inverse square dependence on current density. Considering only the influence of diffusion and electromigration on the vacancy flux, the continuity equation (2.12) along the interconnect length direction can be written as

$$\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}}=\DV\ens... ...s\symCurrDens}{\kB\T}\ensuremath{\ensuremath{\frac{\partial \CV}{\partial x}}},$$ (2.13)

where $\DV$ is the vacancy diffusivity, $\Z$ is the effective charge number, $\ee$ is the elementary charge, $\vec\symElecField$ is the electric field, $\Q$ is the heat of transport, $\symVacRelFactor$ is the vacancy relaxation factor, $\symAtomVol$ is the atomic volume, $\symHydStress$ is the hydrostatic stress, $\kB$ is Boltzmann's constant, and $\T$ is the temperature. Here, the source term $\G = 0$ is used.

For a semi-infinite line under the boundary conditions

$$\CV(-\infty, t) = \Co \quad \textnormal{and} \quad \JV(0, t) = 0,$$ (2.14)

which means that the vacancy concentration at $x=-\infty$ is fixed at an initial equilibrium value, $\Co$, and that there is a perfect blocking boundary ($\JV = 0$) at $x=0$, the solution of (2.13) at the blocking boundary is given by Laplace transformation [50]

$$\frac{\CV(0,t)}{\Co} = 1 + \textnormal{erf}(\beta) + 2\left\lbrac... ...+\textnormal{erf}(\beta)] +\frac{\beta}{\sqrt{\pi}}\exp(-\beta^2)\right\rbrace,$$ (2.15)

where

$$\beta=\frac{\vert\Z\vert \ee\symElecRes\symCurrDens}{2\kB\T}\sqrt{\DV t},$$ (2.16)

and

$$\textnormal{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x \exp(-x^2)\,dt,$$ (2.17)

is the error function.

Assuming that the failure occurs, when the vacancy concentration reaches a given critical value $C_{vf}$ significantly higher than the initial equilibrium value $\Co$, and that $\beta \gg 0$, then (2.15) is approximated [50] by

$$C_{vf}/\Co \approx 4\beta^2 = \left(\frac{\vert\Z\vert \ee\symElecRes\symCurrDens}{\kB\T}\right)^2\DV \TTF.$$ (2.18)

Since the diffusion coefficient is expressed by the Arrhenius law

$$\DV=\DVo\exp\left(-\frac{\Ea}{\kB\T}\right),$$ (2.19)

where $\DVo$ is the pre-exponential factor for vacancy diffusivity, (2.18) yields the mean time to failure of the form

$$\symMTF = \frac{A\T^2}{\symCurrDens^2}\exp\left(\frac{\Ea}{\kB\T}\right).$$ (2.20)

Note that this equation is similar to the original Black's equation (1.5), except for the multiplying term $\T^2$, and it also predicts a mean time to failure with an inverse square current density dependence. This is a result of the assumption that the failure takes place, when the vacancy concentration reaches a given critical value, which corresponds, in fact, to a void nucleation condition.

A similar model to (2.13) had already been proposed by Rosenberg and Ohring [72] including a source term, so that

$$\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}}=\DV\ens... ...ensuremath{\frac{\partial \CV}{\partial x}}} -\frac{\CV - \Co}{\symVacRelTime},$$ (2.21)

where $\Co$ is the equilibrium vacancy concentration and $\symVacRelTime$ is the characteristic vacancy relaxation time. The last term of the right-hand side of this equation represents a source function which models vacancy annihilation and generation. It means that vacancies are annihilated, if their concentration is larger than the equilibrium value, or produced, if their concentration is smaller than the equilibrium one. The vacancy relaxation time, $\symVacRelTime$, characterizes the efficiency of the sites acting as sinks/sources, in such a way that smaller values of $\symVacRelTime$ result in shorter times for the vacancy concentration to reach the steady state condition, and vice versa. As a consequence, high vacancy supersaturation cannot be reached near vacancy sinks, since vacancies are annihilated as soon as the local vacancy concentration becomes higher than its equilibrium value.

The aforementioned models, where material transport only due to gradients of concentration and due to electromigration itself is considered, have two main shortcomings: first, the time scale to reach the steady state vacancy supersaturation lies, at most, in the order of minutes, which is too short compared to the typical failure times. Second, the maximum vacancy supersaturation is very low, in such a way that the energy barrier for void formation would be extremely high. This hinders void formation by means of vacancy condensation and, therefore, a critical vacancy concentration cannot be used to determine the failure of the interconnect. As will be shown in the next sections, these shortcomings can only be resolved with the introduction of mechanical stress in the model equations.