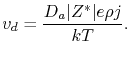2.4.1 The Blech Effect

Blech [75,76,77] designed an experiment where conductor islands were deposited onto a titanium nitride (TiN) film and stressed at a high current density. As the conductor resistivity was much lower than that of the TiN layer, the conductor stripe would carry most of the current and the resulting movement of the ends of the stripe could be measured. In this way, the electromigration induced drift velocity is determined by

$$\symDriftVel = \frac{\DA \vert\Z\vert \ee\symElecRes\symCurrDens}{\kB\T}.$$ (2.22)

Blech observed that only the upstream end (in relation to the electron flow) of the line moved according to (2.22), and that the upstream end stopped moving, when the stripe was reduced to a certain length. Also, he observed that no drift could be detected below a threshold current density.

These observations can be explained by considering the flux due to electromigration and the gradient of the chemical potential via a gradient of mechanical stress [75,76,77,78] according to

$$\JV = \frac{\DV\CV}{\kB\T}\left(\vert\Z\vert \ee\symElecRes\symCu... ...mVol\ensuremath{\ensuremath{\frac{\partial \symHydStress}{\partial x}}}\right),$$ (2.23)

where $\symAtomVol$ is the atomic volume, and $\symHydStress$ is the hydrostatic stress. This equation shows that a gradient of mechanical stress acts as driving force against electromigration. Thus, electromigration stops, when the opposing stress gradient, commonly referred to as ``back stress'', equals the electromigration driving force, so that $\JV = 0$. This steady-state condition is the so-called ``Blech Condition'', given by

$$\ensuremath{\ensuremath{\frac{\partial \symHydStress}{\partial x}}}=\frac{\vert\Z\vert \ee\symElecRes\symCurrDens}{\symAtomVol}.$$ (2.24)

Integrating (2.24) over the length of the interconnect line yields

$$\symHydStress(x) = \sigma_0 + \frac{\vert\Z\vert \ee\symElecRes\symCurrDens}{\symAtomVol}x,$$ (2.25)

where $\sigma_0$ is the stress at $x=0$. This equation shows that the stress varies linearly along the line, when the backflow flux equals the electromigration flux.

Given that the maximum stress the conductor line can withstand is $\symThresholdStress$, a critical product for electromigration failure can be stated as

$$(\symCurrDens \symL)_c = \frac{\symAtomVol(\symThresholdStress - \sigma_0)}{\vert\Z\vert \ee\symElecRes}.$$ (2.26)

This is the so-called ``Blech Product''. The critical product provides a measure of the interconnect resistance against electromigration failure and several experimental works have reported that the critical product for modern copper interconnects is in the range from 2000 to 10000 A/cm [79,80,81,82].

From the above expression, for a given current density, $\symCurrDens$, a critical line length can be determined, so that shorter lines will not fail due to electromigration. This is known as ``Blech Length'', given by

$$\symBlechLength = \frac{\symAtomVol(\symThresholdStress - \sigma_0)}{\vert\Z\vert \ee\symElecRes\symCurrDens}.$$ (2.27)

Similarly, for a given line length, $\symL$, the maximum current density that can be applied for which electromigration failure does not occur is

$$\symCurrDens_c = \frac{\symAtomVol(\symThresholdStress - \sigma_0)}{\vert\Z\vert \ee\symElecRes\symL}.$$ (2.28)

An important consequence of the Blech effect is that the $\symCurrDens\symL$ product during electromigration tests has to be significantly higher than the critical product $(\symCurrDens\symL)_c$ for the corresponding test structure. Otherwise, the test structure might fail at a later time than it would normally do, giving a false sense of safety [83]. Another point to be mentioned is that the presence of residual stresses from the fabrication process reduces the stress which has to be produced by electromigration in order to reach the maximum value a line can withstand. This results in smaller values for the Blech length and for the maximum operating current density than that given by (2.27) and (2.28), respectively [83].