3.5 Mechanical Deformation

It has been shown that material transport due to electromigration produces local strain, which leads to the deformation of the interconnect line. This deformation is described by the displacement field, 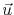$\vec\symDispVec$, of points in the line with respect to a stress-free initial configuration. Assuming that the displacements from the reference configuration are small, the line deformation is characterized by the total strain [151]

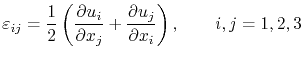$$\symStrain_{ij}=\frac{1}{2}\left(\ensuremath{\frac{\partial \symD... ...uremath{\frac{\partial \symDispVec_j}{\partial x_i}}\right), \qquad i,j = 1,2,3$$ (3.58)

which can be written in matrix notation as

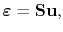$$\boldsymbol\symStrain = \mathbf{S}\mathbf{u},$$ (3.59)

with

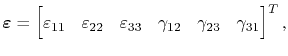$$\boldsymbol\symStrain = \begin{bmatrix}\symStrain_{11} &\symStrain_{22} &\symStrain_{33} &\gamma_{12} &\gamma_{23} &\gamma_{31} \end{bmatrix}^T,$$ (3.60)

where symmetry of the strain tensor is assumed and the engineering shear strains [151]

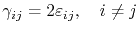$$\gamma_{ij} = 2\symStrain_{ij}, \quad i\neq j$$ (3.61)

are used. The strain operator 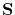$\mathbf{S}$ is given by [151]

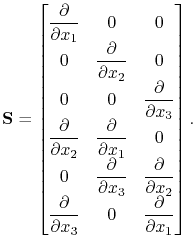$$\mathbf{S} = \begin{bmatrix}\displaystyle\ensuremath{\frac{\parti... ...} &0 &\displaystyle\ensuremath{\frac{\partial }{\partial x_1}}\\ \end{bmatrix}.$$ (3.62)

The total strain has contributions from different sources: the elastic distortion of the line, the thermal strain, and the strain induced by variations in vacancy concentration. Thus, one can write, respectively,

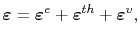$$\boldsymbol\symStrain = \boldsymbol\symStrain^{e} + \boldsymbol\symStrain^{th} + \boldsymbol\symStrain^{v},$$ (3.63)

where

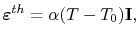$$\boldsymbol{\symStrain}^{th}=\symThermExp(\T - \TO) \mathbf{I},$$ (3.64)

is the thermal strain, and

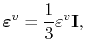$$\boldsymbol\symStrain^{v} = \frac{1}{3}\symStrain^v\mathbf{I},$$ (3.65)

is the electromigration induced strain, with 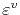$\symStrain^v$ determined from equation (3.42).

Assuming an elastic deformation of the interconnect, which means that Hooke's law applies, the stress is related to the elastic strain by

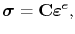$$\boldsymbol\symHydStress = \mathbf{C}\boldsymbol\symStrain^{e},$$ (3.66)

which together with (3.63) yields

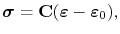$$\boldsymbol\symHydStress = \mathbf{C}(\boldsymbol\symStrain - \boldsymbol\symStrain_{0}),$$ (3.67)

where

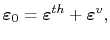$$\boldsymbol\symStrain_{0} = \boldsymbol\symStrain^{th} + \boldsymbol\symStrain^{v},$$ (3.68)

represents the total inelastic strain. Here, the stresses should satisfy the mechanical equilibrium equations [151]

$$\ensuremath{\frac{\partial \symHydStress_{11}}{\partial x_1}}+\en... ...\partial x_2}}+\ensuremath{\frac{\partial \symHydStress_{31}}{\partial x_3}}=0,$$

$$\ensuremath{\frac{\partial \symHydStress_{12}}{\partial x_1}}+\en... ...\partial x_2}}+\ensuremath{\frac{\partial \symHydStress_{32}}{\partial x_3}}=0,$$ (3.69)

$$\ensuremath{\frac{\partial \symHydStress_{13}}{\partial x_1}}+\en... ...\partial x_2}}+\ensuremath{\frac{\partial \symHydStress_{33}}{\partial x_3}}=0,$$

since it is assumed that there are no external forces acting on the line during electromigration. Equation (3.69) can be conveniently expressed by the form

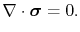$$\ensuremath{\nabla\cdot{\boldsymbol\symHydStress}} = 0.$$ (3.70)