


Next: 4.3.2 Assembly of the
Up: 4.3 Simulation in FEDOS
Previous: 4.3 Simulation in FEDOS
4.3.1 Newton's Method
The non-linear system of equations, which results from the discretization described in Section 4.2, is solved in FEDOS using the conventional Newton method [153,154].
Generally, a non-linear system of 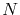 equations is expressed as
equations is expressed as
If a given solution 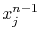 ,
, 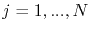 , is known, these equations can expanded in the vicinity of
, is known, these equations can expanded in the vicinity of 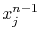 using Taylor's series, which to the first order are approximated by
using Taylor's series, which to the first order are approximated by
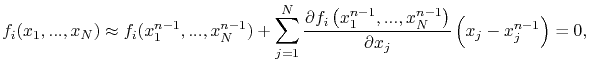 |
(4.69) |
for
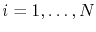 .
The system of equations (4.69) is written in matrix form as
.
The system of equations (4.69) is written in matrix form as
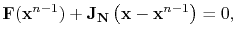 |
(4.70) |
where
 is the so-called Jacobian matrix, for which the entries are given by
is the so-called Jacobian matrix, for which the entries are given by
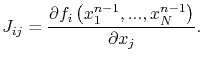 |
(4.71) |
Thus, the solution of (4.70) is
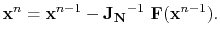 |
(4.72) |
In FEDOS, instead of using (4.72), the linear system of equations
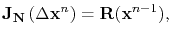 |
(4.73) |
is assembled and solved, so that the increments
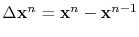 are determined. Here,
are determined. Here,
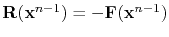 is called residual.
In this way, the new approximate solution
is called residual.
In this way, the new approximate solution
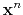 is updated according to
is updated according to
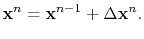 |
(4.74) |
These calculations are performed as an iterative process, where the solution of the 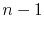 iteration is used to compute the new solution.
The accuracy of the new approximate solution is controlled by the conditions
iteration is used to compute the new solution.
The accuracy of the new approximate solution is controlled by the conditions
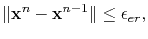 |
(4.75) |
where
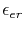 is a given tolerance for the solution error, and
is a given tolerance for the solution error, and
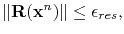 |
(4.76) |
where
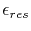 is a given tolerance for the residual and
is a given tolerance for the residual and 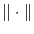 represents the Euclidean norm.
The iterative procedure is terminated, if both criteria are fulfilled.
represents the Euclidean norm.
The iterative procedure is terminated, if both criteria are fulfilled.



Next: 4.3.2 Assembly of the
Up: 4.3 Simulation in FEDOS
Previous: 4.3 Simulation in FEDOS
R. L. de Orio: Electromigration Modeling and Simulation
![]() equations is expressed as
equations is expressed as
![]() iteration is used to compute the new solution.
The accuracy of the new approximate solution is controlled by the conditions
iteration is used to compute the new solution.
The accuracy of the new approximate solution is controlled by the conditions