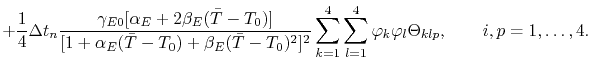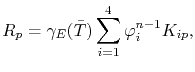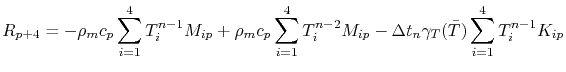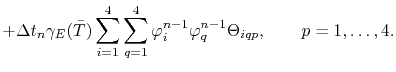


Next: 4.3.3 Assembly of the
Up: 4.3 Simulation in FEDOS
Previous: 4.3.1 Newton's Method
4.3.2 Assembly of the Electro-Thermal Problem
The discretization of the electrical and the thermal problem, (4.32) and (4.40), respectively, forms a non-linear system of equations for a tetrahedral element given by
where
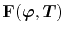 corresponds to
corresponds to
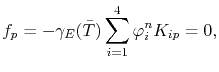 |
(4.78) |
and
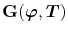 to
to
| |
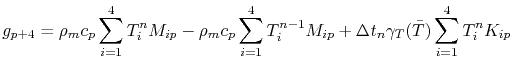 |
|
| |
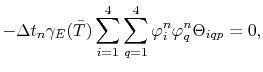 |
(4.79) |
for
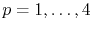 .
.
Applying Newton's method, the element Jacobian matrix for the electro-thermal problem has the form
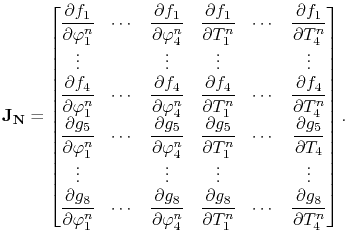 |
(4.80) |
Since the global system for the electro-thermal problem is constructed following the assembly procedure described in Section 4.1.2, the Jacobian matrix is the nucleus matrix to be computed for each element of the mesh.
The matrix entries for the electrical equation (4.78) are given, in general, by
and the entries for the thermal equation (4.79) are computed by
The right-hand side of the linear system (4.73) is assembled by the residuals



Next: 4.3.3 Assembly of the
Up: 4.3 Simulation in FEDOS
Previous: 4.3.1 Newton's Method
R. L. de Orio: Electromigration Modeling and Simulation
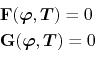
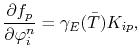
![$\displaystyle \ensuremath{\frac{\partial f_p}{\partial \T_i^n}} = -\ensuremath{...
...T-\TO)+\symQuadTempCoef_E(\bar\T-\TO)^2]^2}\sum_{k=1}^4 \symElecPot_k^n K_{kp},$](img605.png)
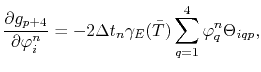
![$\displaystyle \ensuremath{\frac{\partial g_{p+4}}{\partial \T_i^n}} = \symMatDe...
...f_T(\bar\T-\TO)+\symQuadTempCoef_T(\bar\T-\TO)^2]^2} \sum_{k=1}^4 \T_k^n K_{kp}$](img607.png)