[next] [prev] [prev-tail] [tail] [up]

Appendix B
Westergaard Approach

The three crack modes described in Section 4.1 have symmetric and antisymmetric properties. The Westergaard approach permits to easily treat and analyze these kinds of crack problems [70, 71].

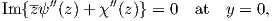
The Westergaard approach is derived for a crack that propagates in Mode I, therefore τxy=0 along y=0.

Using this condition and employing (A.29) we can write

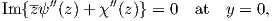Im {zψ ′′(z )+ χ′′(z)} = 0 at y = 0,
(B.1)

which can be satisfied only if

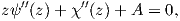zψ ′′(z)+ χ′′(z) + A = 0,
(B.2)

where A is a real constant.

As it is possible to express the stresses and displacements by a single analytic function we write

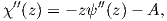′′ ′′ χ (z ) = - zψ (z)- A,
(B.3)

which can be plugged into (A.27) using (A.37). Solving the resulting equation leads to the stresses

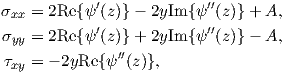′ ′′ σxx = 2Re{ψ (z)}- 2yIm {ψ (z )} + A, σyy = 2Re{ψ ′(z)}+ 2yIm {ψ ′′(z )} - A, τ = - 2yRe {ψ′′(z)}, xy
(B.4)

and the displacements

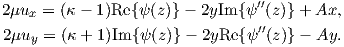′′ 2μux = (κ - 1)Re{ψ (z)} - 2yIm {ψ (z)}+ Ax, 2μuy = (κ + 1)Im{ψ (z)}- 2yRe {ψ′′(z)}- Ay.
(B.5)

If we define

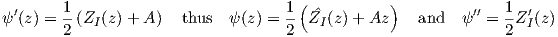ψ′(z) = 1(Z (z)+ A) thus ψ (z) = 1-(Z^ (z) + Az) and ψ ′′ = 1Z ′(z) 2 I 2 I 2 I
(B.6)

where the hat in 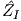ZI(z) indicates the integral ^ ZI′(z) ≡ ZI(z). These equations are further used with (B.4) and (B.5), resulting in

σxx = Re {ZI(z)}- yIm {Z ′I(z)} + 2A, ′ σyy = Re {ZI(z)}+ yIm {Z I(z)}, τxy = - yRe {Z′I(z)}, (κ - 1) 1 2μux = ------Re { ^ZI(z)}- yIm {ZI(z)} +-(κ + 1)Ax, 2 2 2μuy = (κ-+-1)Im { ^ZI(z)}- yRe {ZI(z)} + 1(κ - 3)Ay, 2 2
(B.7)

where A is a uniform uniaxial stress and does not add to the singularity of the stress at the crack tip (usually it is set to 0).

Therefore, the stresses and displacements (B.7) can be derived by choosing the following Airy stress function

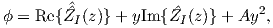ϕ = Re{Z^^I (z)} + yIm{Z^I (z)}+ Ay2,
(B.8)

where the derivatives of the function 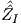Z^^I are defined as

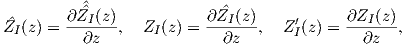∂ ^^ZI(z) ∂Z^I (z) ∂ZI (z) Z^I (z) =-------, ZI(z) = ------, Z ′I(z) =-------, ∂z ∂z ∂z
(B.9)

and ZI(z) is known as Westergaard function.

[next] [prev] [prev-tail] [front] [up]