2.4.2 Electronic Band Structure of SW-CNTs
The electronic structure of a SW-CNT can be obtained from that of
graphene. Assuming periodic boundary conditions in the
circumferential direction characterized by the chiral vector 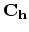 , the wave
vector associated with the
, the wave
vector associated with the 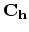 direction becomes quantized, while the
wave-vector associated with the direction of the translational vector
direction becomes quantized, while the
wave-vector associated with the direction of the translational vector 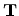 (along the CNT axis) remains continuous for a CNT of infinite length. Thus
the energy bands consist of a set of one-dimensional energy dispersion
relations which are cross sections of those of graphene.
Expressions for the reciprocal lattice vectors
(along the CNT axis) remains continuous for a CNT of infinite length. Thus
the energy bands consist of a set of one-dimensional energy dispersion
relations which are cross sections of those of graphene.
Expressions for the reciprocal lattice vectors 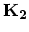 along the
CNT axis, (
along the
CNT axis, (
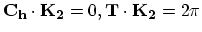 ), and
), and 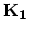 in the circumferential direction, (
in the circumferential direction, (
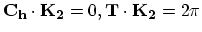 ), are given by (see Table 2.2)
), are given by (see Table 2.2)
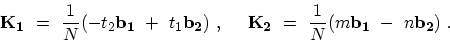 |
(2.5) |
The one-dimensional energy dispersion relations of a SW-CNT can be written as
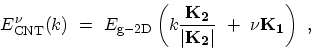 |
(2.6) |
where
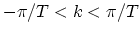 is a one-dimensional wave-vector along the CNT axis and
is a one-dimensional wave-vector along the CNT axis and
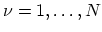 . The periodic boundary condition for a CNT gives
. The periodic boundary condition for a CNT gives  discrete
discrete 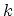 values in the circumferential direction. The N pairs of energy
dispersion curves given by (2.6) correspond to the cross sections of
the two-dimensional energy dispersion surface of graphene. In Fig. 2.7 several cutting
lines near one of the
values in the circumferential direction. The N pairs of energy
dispersion curves given by (2.6) correspond to the cross sections of
the two-dimensional energy dispersion surface of graphene. In Fig. 2.7 several cutting
lines near one of the 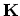 points are shown. The separation between two
adjacent lines and the length of the cutting lines are given by the
points are shown. The separation between two
adjacent lines and the length of the cutting lines are given by the
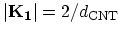 and
and
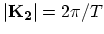 , respectively. If
the cutting line passes through a
, respectively. If
the cutting line passes through a 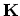 point of
the two-dimensional BRILLOUIN zone (Fig. 2.7-a), where the
point of
the two-dimensional BRILLOUIN zone (Fig. 2.7-a), where the 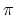 and
and
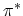 energy bands of graphene are degenerate by symmetry, then the
one-dimensional energy bands have a
zero energy gap. When the
energy bands of graphene are degenerate by symmetry, then the
one-dimensional energy bands have a
zero energy gap. When the 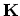 -point is located between to cutting lines,
-point is located between to cutting lines,
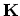 is always located in a position one-third of the distance between
two adjacent
is always located in a position one-third of the distance between
two adjacent 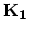 lines (Fig. 2.7-b) [29] and thus a
semiconducting CNT with a finite energy gap is formed. If for a
lines (Fig. 2.7-b) [29] and thus a
semiconducting CNT with a finite energy gap is formed. If for a 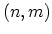 CNT,
CNT,
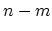 is exactly divisible by 3 the CNT is metallic. CNTs with
residuals 1 and 2 of the division
is exactly divisible by 3 the CNT is metallic. CNTs with
residuals 1 and 2 of the division 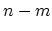 by 3 are
semiconducting.
by 3 are
semiconducting.
Figure 2.7:
The one-dimensional wave-vectors 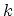 are
shown in the BRILLOUIN zone of graphene as bold lines for
(a) metallic and (b) semiconducting CNTs.
are
shown in the BRILLOUIN zone of graphene as bold lines for
(a) metallic and (b) semiconducting CNTs.
|
|
Figure 2.8:
One-dimensional energy dispersion relations of a)
the 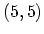 armchair CNT, b) the
armchair CNT, b) the 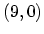 zigzag CNT, and c) the
zigzag CNT, and c) the 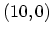 zigzag CNT.
zigzag CNT.
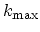 for armchair and zigzag CNTs correspond to
for armchair and zigzag CNTs correspond to
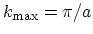 and
and
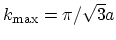 , respectively.
Solid lines denote degenerate bands and dashed lines non-degenerate bands.
, respectively.
Solid lines denote degenerate bands and dashed lines non-degenerate bands.
|
|
Figure 2.8 shows the energy dispersion relations for the 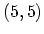 armchair, the
armchair, the 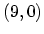 zigzag, and the
zigzag, and the 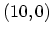 zigzag CNTs. In general
zigzag CNTs. In general 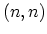 armchair CNTs yield
armchair CNTs yield 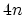 energy subbands with
energy subbands with 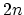 conduction and
conduction and 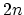 valence
bands. Of these
valence
bands. Of these 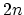 bands, two are non-degenerate and
bands, two are non-degenerate and 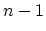 are doubly
degenerate. The degeneracy comes from the two subbands with the same energy
dispersion, but different
are doubly
degenerate. The degeneracy comes from the two subbands with the same energy
dispersion, but different 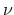 -values. All armchair CNTs have a band
degeneracy between the highest valence and the lowest conduction band
(Fig. 2.8-a). In zigzag CNTs the lowest conduction and the highest
valence bands are doubly degenerate (Fig. 2.8-b and Fig. 2.8-c).
-values. All armchair CNTs have a band
degeneracy between the highest valence and the lowest conduction band
(Fig. 2.8-a). In zigzag CNTs the lowest conduction and the highest
valence bands are doubly degenerate (Fig. 2.8-b and Fig. 2.8-c).
In armchair and zigzag CNTs the bands are symmetric with respect to
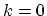 . Since the band of an armchair CNT has a minimum at point
. Since the band of an armchair CNT has a minimum at point 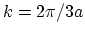 , it
has a mirror minimum at point
, it
has a mirror minimum at point
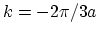 and therefore two equivalent valleys
are present around the point
and therefore two equivalent valleys
are present around the point
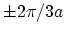 . The bands of zigzag and chiral
CNTs can have at most one valley (Fig. 2.8-b and Fig. 2.8-c).
. The bands of zigzag and chiral
CNTs can have at most one valley (Fig. 2.8-b and Fig. 2.8-c).
In armchair CNTs the bands cross the FERMI level at
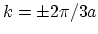 . Thus,
all they are expected to exhibit metallic conduction [12]. There
is no energy gap for the
. Thus,
all they are expected to exhibit metallic conduction [12]. There
is no energy gap for the 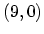 CNT at
CNT at 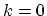 , whereas the
, whereas the 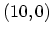 CNT indeed
shows an energy gap.
CNT indeed
shows an energy gap.
Electrical conduction is determined by states around the FERMI energy. Therefore,
it is useful to develop an approximate relation that describes the dispersion
relations in the regions around the FERMI energy
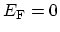 . This can be
done by replacing the expression for
. This can be
done by replacing the expression for
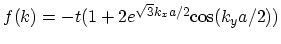 in (2.3) with a TAYLOR expansion around the point
in (2.3) with a TAYLOR expansion around the point
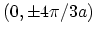 where the energy gap is zero and
where the energy gap is zero and 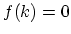 . It is straightforward to
show that
. It is straightforward to
show that
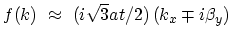 ,
with
,
with
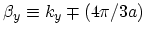 . The corresponding energy dispersion
relation can be written as [33]
. The corresponding energy dispersion
relation can be written as [33]
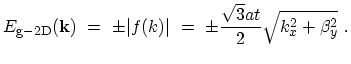 |
(2.7) |
The energy bands for  zigzag CNTs can be obtained by imposing the
periodic boundary conditions, which define the number of allowed wave-vectors
zigzag CNTs can be obtained by imposing the
periodic boundary conditions, which define the number of allowed wave-vectors  in
the circumferential direction as
in
the circumferential direction as
 . This yields
the one-dimensional dispersion relations for the
. This yields
the one-dimensional dispersion relations for the 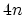 states of the
states of the 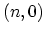 zigzag CNT
zigzag CNT
![$\displaystyle E^{\nu}(k_x) \ = \ \pm \frac{\sqrt{3}at}{2} \sqrt{k_x^2\ +\ {\lef...
...ac{3\nu}{2n}-1\right)\right]}^2} \ , \ \ \ -\pi/\sqrt{3}a<k_x<\pi/\sqrt{3}a \ .$](img284.png) |
(2.8) |
Therefore, the energy gap for
subband 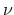 can be written as difference between the energies of the
can be written as difference between the energies of the 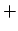 and
and 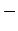 branches at
branches at 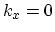
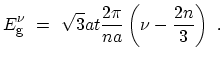 |
(2.9) |
The energy gap has a minimum value of zero corresponding to 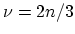 .
If
.
If 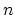 is not a multiple of three the minimum value of
is not a multiple of three the minimum value of  is equal to
is equal to
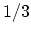 . This means that the minimum energy gap is then given by
. This means that the minimum energy gap is then given by
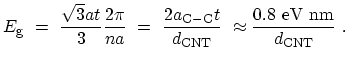 |
(2.10) |
where
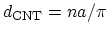 is the diameter of the CNT in nano-meters.
Based on (2.8) and (2.9), the DOS for semiconducting
zigzag CNTs is given by
is the diameter of the CNT in nano-meters.
Based on (2.8) and (2.9), the DOS for semiconducting
zigzag CNTs is given by
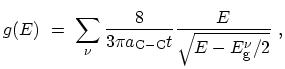 |
(2.11) |
which is an approximation valid as long as
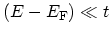 [34]. VAN HOVE singularities in the DOS appearing
at both the energy minima and maxima of the bands
(see Fig. 2.9) are important for determining various solid-state
properties of CNTs [35,36]
[34]. VAN HOVE singularities in the DOS appearing
at both the energy minima and maxima of the bands
(see Fig. 2.9) are important for determining various solid-state
properties of CNTs [35,36]
For all metallic CNTs, independent of their diameter and chirality, due to the
nearly linear dispersion relations around the FERMI energy the density of
states (DOS) per unit length along the CNT axis is a constant given by
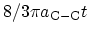 [12].
[12].
Figure 2.9:
The density of states per unit cell of graphene
for a) the  zigzag CNT which has metallic behavior and b)
the
zigzag CNT which has metallic behavior and b)
the 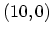 zigzag CNT which has semiconducting behavior. Dashed lines
show the density of states for the graphene sheet [21].
zigzag CNT which has semiconducting behavior. Dashed lines
show the density of states for the graphene sheet [21].
|
|
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![\includegraphics[width=.33\textwidth]{figures/Bri_CNT_Metal.eps}](img258.png)
![\includegraphics[width=.33\textwidth]{figures/Bri_CNT_Semi.eps}](img259.png)
![\includegraphics[width=.31\textwidth]{figures/Ek-5-5.eps}](img263.png)
![\includegraphics[width=.31\textwidth]{figures/Ek-9-0.eps}](img264.png)
![\includegraphics[width=.31\textwidth]{figures/Ek-10-0.eps}](img265.png)
![]() armchair, the
armchair, the ![]() zigzag, and the
zigzag, and the ![]() zigzag CNTs. In general
zigzag CNTs. In general ![]() armchair CNTs yield
armchair CNTs yield ![]() energy subbands with
energy subbands with ![]() conduction and
conduction and ![]() valence
bands. Of these
valence
bands. Of these ![]() bands, two are non-degenerate and
bands, two are non-degenerate and ![]() are doubly
degenerate. The degeneracy comes from the two subbands with the same energy
dispersion, but different
are doubly
degenerate. The degeneracy comes from the two subbands with the same energy
dispersion, but different ![]() -values. All armchair CNTs have a band
degeneracy between the highest valence and the lowest conduction band
(Fig. 2.8-a). In zigzag CNTs the lowest conduction and the highest
valence bands are doubly degenerate (Fig. 2.8-b and Fig. 2.8-c).
-values. All armchair CNTs have a band
degeneracy between the highest valence and the lowest conduction band
(Fig. 2.8-a). In zigzag CNTs the lowest conduction and the highest
valence bands are doubly degenerate (Fig. 2.8-b and Fig. 2.8-c).
![]() . Since the band of an armchair CNT has a minimum at point
. Since the band of an armchair CNT has a minimum at point ![]() , it
has a mirror minimum at point
, it
has a mirror minimum at point
![]() and therefore two equivalent valleys
are present around the point
and therefore two equivalent valleys
are present around the point
![]() . The bands of zigzag and chiral
CNTs can have at most one valley (Fig. 2.8-b and Fig. 2.8-c).
. The bands of zigzag and chiral
CNTs can have at most one valley (Fig. 2.8-b and Fig. 2.8-c).
![]() . Thus,
all they are expected to exhibit metallic conduction [12]. There
is no energy gap for the
. Thus,
all they are expected to exhibit metallic conduction [12]. There
is no energy gap for the ![]() CNT at
CNT at ![]() , whereas the
, whereas the ![]() CNT indeed
shows an energy gap.
CNT indeed
shows an energy gap.
![]() . This can be
done by replacing the expression for
. This can be
done by replacing the expression for
![]() in (2.3) with a TAYLOR expansion around the point
in (2.3) with a TAYLOR expansion around the point
![]() where the energy gap is zero and
where the energy gap is zero and ![]() . It is straightforward to
show that
. It is straightforward to
show that
![]() ,
with
,
with
![]() . The corresponding energy dispersion
relation can be written as [33]
. The corresponding energy dispersion
relation can be written as [33]
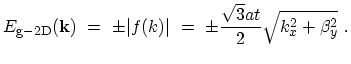
![]() [12].
[12].
![\includegraphics[width=.36\textwidth]{figures/DOS-9-0.eps}](img297.png)
![\includegraphics[width=.36\textwidth]{figures/DOS-10-0.eps}](img298.png)