4.6 Scattering Self-Energies
The lowest-order electron-phonon self-energies are introduced in
Section 3.6 and the steady-state form of these self-energies has been
derived in Section 3.8.3. By transforming the
self-energies (3.73) into mode-space
one obtains [10]
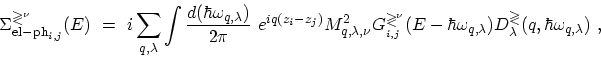 |
(4.35) |
where 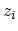 is the position of some lattice point
is the position of some lattice point 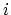 along the CNT axis. Note that due
to the one-dimensional nature of CNTs, the coordinate and wave-vector variables
are all one-dimensional. In (4.35) only intra-subband scattering
process are considered (see Section 2.6). To include inter-subband
scattering processes the summation in (4.35) would have to run over the
all subbands
along the CNT axis. Note that due
to the one-dimensional nature of CNTs, the coordinate and wave-vector variables
are all one-dimensional. In (4.35) only intra-subband scattering
process are considered (see Section 2.6). To include inter-subband
scattering processes the summation in (4.35) would have to run over the
all subbands 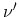 with the electron-phonon matrix elements
with the electron-phonon matrix elements
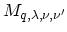 .
.
The electron-phonon self-energies in the self-consistent BORN approximation are
expressed in terms of the full electron and phonon GREEN's functions.
One should therefore study the influence of the
bare electron states on the phonons first, and then calculate the effect on
the electrons of the renormalized phonon states [190]. In this
work we assume that the phonon renormalization can be neglected. By doing so
we miss to capture a possible reduction of the phonon lifetime. The above
considerations also appeal to the MIGDAL theorem [246]
which states that the phonon-induced renormalization of the electron-phonon
vertex (see Appendix F.2) scales with the ratio of the electron mass to the ion
mass [189]. Therefore, one can assume that the phonon bath is
in thermal equilibrium so that the full phonon GREEN's function 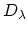 can be replaced by the non-interacting GREEN's functions
can be replaced by the non-interacting GREEN's functions
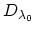 from (D.16). As a result (4.35) can be
written as
from (D.16). As a result (4.35) can be
written as
![\begin{displaymath}\begin{array}{ll}\displaystyle \Sigma_{\mathrm{el-ph}_{i,j}}^...
...G_{_{i,j}}^{<^\nu}(E-\hbar\omega_{q,\lambda}) ] \ , \end{array}\end{displaymath}](img839.png) |
(4.36) |
![\begin{displaymath}\begin{array}{ll}\displaystyle \Sigma_{\mathrm{el-ph}_{i,j}}^...
...G_{_{i,j}}^{>^\nu}(E+\hbar\omega_{q,\lambda}) ] \ , \end{array}\end{displaymath}](img840.png) |
(4.37) |
where the first term on the right hand side is due to phonon emission and the
second term due to phonon absorption. The summation over wave-vector 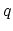 in (4.36) and (4.37) can be generally transformed
into an integral over the first
BRILLOUIN zone
in (4.36) and (4.37) can be generally transformed
into an integral over the first
BRILLOUIN zone
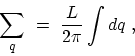 |
(4.38) |
where 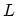 is the normalization length and the limits of the integral are
is the normalization length and the limits of the integral are
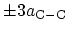 which is the period of the carbon rings,
see (4.3). To calculate electron-phonon self-energies the
integral in (4.38) must be evaluated.
which is the period of the carbon rings,
see (4.3). To calculate electron-phonon self-energies the
integral in (4.38) must be evaluated.
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() can be replaced by the non-interacting GREEN's functions
can be replaced by the non-interacting GREEN's functions
![]() from (D.16). As a result (4.35) can be
written as
from (D.16). As a result (4.35) can be
written as