2.2 The Structuring Element Algorithm

The geometry is represented by an array of cubic cells which have a unique material index. The surface is represented as list of all material cells which are adjacent to vacuum cells. The surface propagation is carried out by applying a so called structuring element to the surface. The shape of the structuring elements depends on the process to be modeled and for each time-step their size which represents the local etching or deposition rate is calculated for each surface cell. Since the structuring element is discretized in the same cellular format as the geometry, applying the structuring elements means marking of all cells which are hit by the elements. After each time-step, the indices of the marked material cells are updated, either from the material index to 0 which denotes vacuum cells or from 0 to the index of the newly deposited material. Then, the new surface is extracted and again size and orientation of the structuring elements are calculated and applied to the new surface until the overall simulation time is completed.

**Figure 2.1:** Material representation and structuring element for isotropic etching.
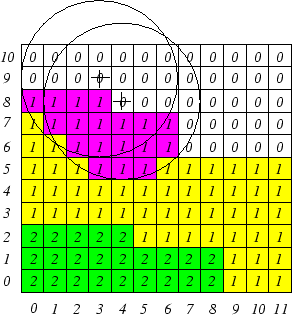
$\begin{figure}\begin{center} \ifthenelse{\boolean{nopics}}{\fbox{\texttt{eps-al/... ...ox{!}{7cm}{\includegraphics{eps-al/materials-col.eps}}} \end{center}\end{figure}$

This rather abstract description is illustrated in Fig. 2.1 for an isotropic etching step. Since it is more obvious, a two-dimensional example was chosen. The geometry is composed of two materials, suppose silicon (2) and silicon oxide (1). Isotropic etching means that the etching velocity at a specific position at the surface is the same in all directions. This can be described by a circle, composing the structuring element for an isotropic step. In the figure only two structuring elements are applied at cell (3,9) and (4,8), for the complete simulation this is done for all surface cells. In this way the structuring element is moved along the surface, similarly to the use of brushes in image processing. All material cells whose center is located within at least one of the circles are marked, illustrated in the figure by the purple cells. After the marking procedure is completed for all surface positions, the material index of the purple (marked) cells is set to 0. They are etched away within this time-step. This leads to an updated geometry and a new set of surface positions. Newly calculated structuring elements are applied to the new surface positions which is repeated until the simulation time is completed.

Two important aspects of this methodology are worth to be mentioned. The first is that it can be applied in the same manner to etching and deposition. The only difference is, that for a deposition step the vacuum cells within the circles have to be painted purple and must be set to the index of the deposited material. The left hand side of Fig. 2.2 shows how one and the same isotropic structuring elements applied at the same initial surface can be used for the profile evolution of etching and deposition processes.

**Figure 2.2:** Structuring elements suited both for etching *and* deposition processes (left) as well as for many different process models (right).
$\begin{figure}\psfrag{t}[][]{$t$} \psfrag{t + dt}[][]{$t + dt$} \begin{center} \... ...width}{!}{\includegraphics{eps-al/uni-depo.eps}}\hfill} \end{center}\end{figure}$

The second advantage is that this technique covers a wide range of models for possible etching and deposition processes just by changing shape, orientation, and size of the structuring element as indicated on the right hand side of Fig. 2.2 with a directional deposition step which has to include visibility testing.

In the general three-dimensional case the structuring element is an ellipsoidal with the three diameters

, and

. Its orientation is specified by a polar angle $\varphi$ and an azimuthal angle $\vartheta$ . This general form of the structuring element is used to model reactive ion etching and sputter deposition where the local rates depend on the visibility conditions and are calculated as integral of the particle distribution function over the visible solid angle. For simple anisotropic models, the main axis of the ellipsoidal is fixed to a vertical direction and its size is given by a vertical rate

and a lateral rate

. For the isotropic case all three diameters are equal

, the ellipsoidal develops to a sphere, and the orientation becomes insignificant.

This should be enough in order to demonstrate the basic ability for very flexible modeling provided by the cellular structuring element approach. Detailed descriptions on how this method is applied to a wide range of topography simulations will be given throughout the thesis, e.g., in Section 3.2 for the basic topography simulation steps, in Chapter 6 for detailed modeling of low-pressure etching and deposition processes, and in Chapter 7 for high-pressure chemical vapor deposition. But before going into the detailed explanation of the models, extensions and optimizations for the basic structuring element implementation will be introduced.