


Prev: 2.3.1 Spherical Segment Elements
Up: 2.3 Optimizations for the
Next: 2.3.3 Benchmark Example and
2.3.2 Line Elements
A further possibility for CPU time reduction is the restriction to exclusive
application of lines as structuring elements. The length of the lines is
determined by the deposition rate multiplied with the time-step. In case of
isotropic deposition the growth direction is perpendicular to the surface,
therefore the surface orientation which is not implicitly given in the cellular
material representation has to be calculated. The calculation of the
orientation of a surface cell is done by averaging the normals of the cube
faces of all surface cells within a certain distance 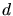 from the considered
surface cell. Averaging alone would give wrong results where planar faces
intersect, since the surface normals of surface cells located within averaging
distance
from the considered
surface cell. Averaging alone would give wrong results where planar faces
intersect, since the surface normals of surface cells located within averaging
distance 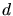 from an intersection would already start to incline towards the
normal of the second plane. This can be seen at the convex corner of the
initial (lowest) geometry and at the concave corners on the left hand side
of Fig. 2.5, which depicts the unit surface normal vectors for the surface
cells of a cylindrical via for two time-steps of an isotropic deposition. By
means of a special edge detection algorithm it is possible to conserve sharp
corners of the geometry, which otherwise would be rounded by the averaging
algorithm. The right hand side in Fig. 2.5 shows the surface normals
corrected in this way for the same cylindric via structure.
from an intersection would already start to incline towards the
normal of the second plane. This can be seen at the convex corner of the
initial (lowest) geometry and at the concave corners on the left hand side
of Fig. 2.5, which depicts the unit surface normal vectors for the surface
cells of a cylindrical via for two time-steps of an isotropic deposition. By
means of a special edge detection algorithm it is possible to conserve sharp
corners of the geometry, which otherwise would be rounded by the averaging
algorithm. The right hand side in Fig. 2.5 shows the surface normals
corrected in this way for the same cylindric via structure.
Figure 2.5:
Surface normals for three different time-steps of isotropic deposition into a
cylindrically shaped via. The surface normals resulting from an averaging
algorithm without edge correction are shown on the left hand side. The edge
detection applied on the right hand side conserves the vertical and horizontal
surface normals at the edges of the initial geometry.
 |
The line element method is similar to ray-tracing topography algorithms.
If the lines corresponding to the rays are dense enough with respect to the
cellular geometry representation, a smooth surface is assured. Special care has
to be taken at corners or edges where the line elements have to be applied
repeatedly with directions interpolated between the surface orientation of the
adjacent cells for assuring a smooth and continuous surface. The interpolation
at edges is completely different from the averaging method used for the
calculation of the surface normals (see left hand side of Fig. 2.5). Using
the uncorrected, averaged surface normals would not correctly reproduce the
isotropically deposited layer.
In contrast to the spherical segment algorithm introduced before, this
algorithm performs better for curved surfaces. Only cells very close to the
surface are hit repeatedly when interpolation is necessary at curved
regions. The right hand side of Fig. 2.4 where the linear
structuring elements are applied at the same positions as the spherical
segments on the left hand side, gives an idea of the further reduction of
redundant operations achievable with this algorithm.



Prev: 2.3.1 Spherical Segment Elements
Up: 2.3 Optimizations for the
Next: 2.3.3 Benchmark Example and
W. Pyka: Feature Scale Modeling for Etching and
Deposition Processes in Semiconductor Manufacturing


![]()
![]()
![]()
![]()