Prev: 6.2.2 Plasma Deposition

6.2.3 Sputter Deposition

In this section a simulation model for physical sputter deposition will be introduced. A fitting model which gives a phenomenological description of the overall film evolution is used here instead of tracing and estimating direct and reflected contributions of different kind of particles, as done for the reactive ion etching and plasma deposition above. The details of the model and how it was calibrated for the simulation of ${\rm TiN}$ magnetron sputter deposition will be shown in the following.

In current integrated circuits contacts have to fulfill a long list of requirements: The contact resistivity has to be low, the metallurgical isolation which prohibits the diffusion of the contact metal into the silicon has to be guaranteed, the adhesion has to be sufficient, and leakage free film formation as well as void free filling has to be assured. It is clear, that the complete list cannot be fulfilled by a single material but only by a compound of different layers which perform different tasks. For metal stacks used for tungsten plug fills, ${\rm TiN}$ has been recognized as excellent barrier material and is used as nucleation/glue layer at the contact/via level as well as a diffusion barrier and anti-reflection coating in the interconnect stack [14].

Several physical vapor deposition techniques, such as magnetron sputter deposition [58], collimated sputtering [61], and reactive sputtering [11] as well as chemical vapor deposition techniques [15] exist for the deposition of ${\rm TiN}$ and are selected depending on the purpose of the layer. Our general approach can model different physical deposition techniques, since it approximates the particle distributions arriving at the wafer surface, regardless of the processes occurring in the reactor chamber, which are responsible for the incidence characteristics.

As explained in Section 6.1.4 a detailed model taking into account direct and reflected contributions of different types of particles results in a huge amount of distribution and interaction parameters which are usually hard to assess. Therefore an overall fitting approach was selected in order to model magnetron sputter deposition.

The ${\rm Ti}$ particles ejected from the target react with the argon/nitrogen plasma and arrive at the wafer surface as ${\rm TiN}$ particles. According to the reactor configuration from Fig. 6.4 with the circular racetrack in the sputter target (6.4) was used to approximate the incoming distribution of the ${\rm TiN}$ particles. The equation was extended to

$${\mathrm F}(\varphi, \vartheta) = a \vartheta^3 e^{-b \vartheta} + c (1 - e^{-d \vartheta} )$$ (6.15)

where the additive term $c (1 - e^{-d \vartheta})$ represents a contribution of lateral particle incidence necessary in order to obtain a sufficiently large sidewall coverage as observed experimentally. Within the phenomenological approach this additive term is not directly coupled to a specific particle fraction but can be interpreted as laterally incident, low energetic particles at the top of the feature, arriving directly from the reactor chamber as well as particles reflected from the sidewall.

Thus, there are only two free parameters left for the distribution function. The first one is the angle of maximum particle incidence, which is converted to the parameters $a$ and $b$ in (6.15). As a first approximation this angle is given by the direction of the maximum depth in the target erosion profile seen from the center of the wafer. Due to the uncertainty in the determination of the maximum of the shallow erosion profile and the additional collisions of the particles on their way from the target to the wafer, the angle does not necessarily correspond to the geometric angle and was left as a variable for the following optimization. The second parameter is the fraction of low energy particles, given by the parameter $c$. $d$ in (6.15) is kept constant at a value of 5 accounting for a fast increase of the low energy fraction from 0 for normal incidence to its nominal value $c$ for an incidence angle of 90$^\circ$.

Figure 6.15: Particle distribution functions for different sets of parameters for the angle of maximum particle incidence and for the fraction of the low energy particles.

Fig. 6.15 shows three set of curves for distribution functions which represent different process pressures (cf. Section 6.1.2). The solid lines represent the overall distribution function according to (6.15), which is composed by the contribution of (6.4) (dashed lines) plus the additive term for the low energy particle fraction (dotted lines).

With this one-species model the barrier layer formation for a series of vias with different diameters ranging from 0.3$\mu\mathrm m$ to 1.0$\mu\mathrm m$ was simulated at a center wafer position and 90mm off the wafer center. The deposition was performed at a deposition rate of 33.8nm/min for 320s. The depth of the vias is 1.3$\mu\mathrm m$ for all diameters. The final goal of the simulations was to calibrate the model with experimentally obtained profiles for the circular vias and to subsequently use the calibrated model to predict possible leakages in the barrier layer formation when applying the same process technology to a damascene structure. The pressure for the experiments was 2.3mTorr, which matches exactly the pressure region for the MC particle transport simulations from [46], building the base for the assumed distribution function.

For the calibration with the optimization tool SIESTA [54][76], the simulation results of the 1.0$\mu\mathrm m$ structure were compared with experimentally obtained film thicknesses extracted from SEM cross-sections. This was done for the center wafer position as well as for the off-center position. The calibration was restricted to the 1.0$\mu\mathrm m$ structure because it shows the largest film thickness and hence introduces the lowest error in the measurement of the profiles. Furthermore the restriction to one diameter allowed the validation of the calibration with the other four diameters (0.3, 0.4, 0.5, and 0.7$\mu\mathrm m$).

By adjusting the two free parameters of the distribution function, namely, the angle of maximum particle incidence and the fraction of laterally incident particles, the optimization minimizes the difference between calculated film thicknesses and thicknesses extracted from the SEM profiles. The results from the optimization are 9.2$^\circ$ for the angular position of the maximum in the distribution function and 0.12 for the fraction of lateral particles.

Figure 6.16: Deposition of ${\rm TiN}$ into 0.4$\mu\mathrm m$ and 0.7$\mu\mathrm m$ diameter, 1.3$\mu\mathrm m$ deep vias. The upper row shows the center wafer position, the lower row a position 90mm off the wafer center. The deposition rate is 33.8nm/min and the simulation time 320s.

Fig. 6.16 compares simulated and experimental cross-sections for the structures with 0.4 and 0.7$\mu\mathrm m$ diameter. The simulations have been carried out with the parameters obtained from the calibration with the 1.0$\mu\mathrm m$ structure. It is clear, that the calibrated 1.0$\mu\mathrm m$ structure exactly matches the SEM cross-sections, therefore the comparison is omitted. The figures for the simulation results are cross-sections through the three-dimensional simulation domains. Three-dimensional simulations were necessary for the correct visibility conditions for the three-dimensional distribution functions. The cross-sections were extracted with an auxiliary function of the solid modeling tool introduced in Chapter 3.

The figures demonstrate, that the simulated profiles are in excellent agreement with the SEM cross-sections. The simulation results represent the downward decrease in the sidewall thickness as well as the curvature at the bottom of the via. The figures in the upper row show the center wafer position with radially symmetric profiles. The lower row demonstrates the results for the position 90mm off the wafer center. The right side of the structures is exposed towards the slanted particle flux, whereas for the sidewall on the left hand side a major part of the flux is screened, which leads to a strongly asymmetric profile. Regardless of the polar position of the radially symmetric structures, the side which is facing towards the center of the wafer exhibits the larger thickness, the side looking away from the wafer center resides in the shadow of the flux, which leads to a lower film thickness.

For the constant depth of 1.3$\mu\mathrm m$ for the vias, the aspect ratio defined as the ratio between depth and width of the structure increases for decreasing diameters of the vias and the opening angle towards the particle source decreases. In consequence, the film thickness at the bottom is decreasing when the diameter becomes smaller. Still, bottom coverage is assured for all diameters and the deposited film is thick enough to insure a sufficient barrier function of the layer.

With the same parameters, a damascene structure consisting of a 0.3$\mu\mathrm m$ diameter, 0.7$\mu\mathrm m$ deep hole in a 0.3$\mu\mathrm m$ wide, 0.5$\mu\mathrm m$ deep rectangular trench was simulated. For this structure which combines a radially symmetric feature with a trench considered as infinitely long, a three-dimensional simulation is absolutely necessary. Furthermore the orientation of the trench with respect to the main particle incidence and thus the polar position $\varphi$ of the structure on the wafer is of significant influence.

Figure 6.17: Positions of the two simulated damascene structures on the wafer and cutting directions parallel and perpendicular to the trench for the cross-sections shown in Fig. 6.18.

For these reasons, the damascene structure has been simulated for different positions on the wafer. The most pronounced differences can be found between the two positions shown in Fig. 6.17. Pos.1 is located at a peripheral position right from the wafer center. Thus, the main particle incidence for this position (indicated in the figure by the thick, black arrow) is oriented perpendicularly to the trench. This is opposed to Pos.2 which is located behind the wafer center. In this case the orientation of the trench is the same as for Pos.1, but since the particle incidence predominantly originating from the center of the wafer changes its direction, the flux is now oriented parallelly to the trench.

Figure 6.18: Damascene structure with perpendicular and parallel direction of main particle incidence.

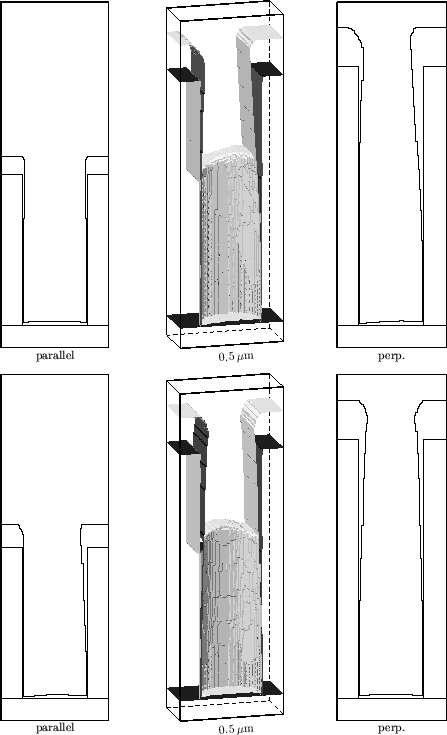Fig. 6.18 shows the simulation results for the damascene structure at the two different off-center positions. For both positions the resulting three-dimensional topography and cross-sections parallel (left) and perpendicular (right) to the trench are shown. For the direction and the position of the cross-sections refer to Fig. 6.17. The three figures in the upper row represent Pos.1, the other three figures stand for a damascene structure at Pos.2.

The resulting minimum film thickness at the bottom of the features is 15nm, giving a sufficient isolation to the underlying silicon substrate, which is the goal for the barrier layer formation. The sidewall coverage is very poor. In the bottom corner region at the shadowed sides it becomes $<$5nm and continuous sidewall coverage can not be guaranteed. Fortunately this is not a necessary requirement for the process since the damascene structure is etched into a silicon-dioxide layer deposited on the silicon substrate. Therefore the isolation to the silicon-dioxide is of secondary importance.

The figures in the upper row of Fig. 6.18 for the perpendicular particle incidence show that the cross-section parallel to the trench is symmetrical, whereas the cross-section perpendicular to the trench reveals asymmetry caused by the stronger exposure of the right sidewall to the particle flux. For the parallel particle incidence the effect is vice versa. For all structures including the circular vias, the regions most probable for an insufficient coverage are the sidewalls turned away from the center of the sputter target, where a major part of the incoming particles is screened.

The simulations have shown that the analytical particle distributions and the model for the definition of the position of the structures on the wafer by setting the polar ( $\varphi_{\mathrm{src}}$) and azimuthal ( $\vartheta_{\mathrm{src}}$) angle of the origin of the particle distribution function allow predictive simulations of low-pressure etching and deposition processes.

Prev: 6.2.2 Plasma Deposition