

Next: 7.6.2 Technology F: Metamorphic Depletion
Up: 7.6 Technologies Based on
Previous: 7.6 Technologies Based on
InAlAs/InGaAs HEMTs based on InP substrates are the fastest three
terminal devices existing. However, there are several aspects to
be accounted for in order to reliably use these devices in
applications. Fig. 7.35 shows the transfer curve for a
split channel
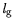 = 150 nm
In
= 150 nm
In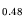 AlAs/In
AlAs/In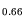 Ga
Ga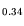 As/InP device as a function
of temperature
As/InP device as a function
of temperature
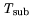 . For the applied
. For the applied
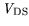 = 0.75 V, the
device shows a DC-
= 0.75 V, the
device shows a DC-
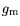 of nearly 1000 mS/mm. The transfer
characteristics further shows a decrease of
of nearly 1000 mS/mm. The transfer
characteristics further shows a decrease of
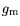 and
and
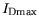 with rising temperature.
with rising temperature.
Figure 7.35:
Simulated and measured transfer
characteristic as a function of temperature 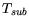 .
.
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig58.eps}](img880.gif)
|
Figure 7.36:
Output characteristics of a dual
channel InP based pseudomorphic HEMT with 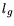 = 150 nm.
= 150 nm.
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig59.eps}](img881.gif)
|
Fig. 7.36 shows the corresponding output characteristics and comparison with
measurements for
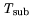 = 300 K. For the ohmic contacts Case I in Fig. 3.25 is assumed in
the model based on geometry information. Very good agreement is found for this device between
simulation and measurements based on the model parameter values given in Chapter 3. As a basic
result, the output conductance cannot be understood without taking electrons and holes and their
generation/recombination into account. Four factors are found significant for this high
gain device and to be responsible for the output conductance in this static simulation analysis.
The transient behavior of the generation/recombination is not included.
= 300 K. For the ohmic contacts Case I in Fig. 3.25 is assumed in
the model based on geometry information. Very good agreement is found for this device between
simulation and measurements based on the model parameter values given in Chapter 3. As a basic
result, the output conductance cannot be understood without taking electrons and holes and their
generation/recombination into account. Four factors are found significant for this high
gain device and to be responsible for the output conductance in this static simulation analysis.
The transient behavior of the generation/recombination is not included.
- Surface potential/surface charges.
- Source recess geometry
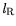 .
.
- Generation/recombination.
- Impact ionization.
The output conductance
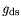 is often discussed related to the
term ''kink'' [281]. The analysis performed for the
simulations in Fig. 7.36 show that a kink is only a very
special combination of the factors to influence the conductance
is often discussed related to the
term ''kink'' [281]. The analysis performed for the
simulations in Fig. 7.36 show that a kink is only a very
special combination of the factors to influence the conductance
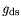 [281]. The factors have their influence even if
a ''kink'' is not visible at all. The surface potential for
In
[281]. The factors have their influence even if
a ''kink'' is not visible at all. The surface potential for
In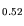 Al
Al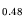 As is only subject to minor changes due to
the pinning of the Fermi level, if a stable surface treatment and
SiN passivation is provided. The complete geometry of the source
side influences the current flow. First, for the pinned surface
potential at the SiN/InAlAs interface, a depletion region
prevails near the surface at both source and drain, which attracts
holes from the material background concentration and the manifold
generation processes (SRH, impact ionization, Auger). This
results in a change of the source side potential near the gate
and thus in changes in the currents
As is only subject to minor changes due to
the pinning of the Fermi level, if a stable surface treatment and
SiN passivation is provided. The complete geometry of the source
side influences the current flow. First, for the pinned surface
potential at the SiN/InAlAs interface, a depletion region
prevails near the surface at both source and drain, which attracts
holes from the material background concentration and the manifold
generation processes (SRH, impact ionization, Auger). This
results in a change of the source side potential near the gate
and thus in changes in the currents
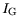 and
and
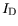 . Second, and
especially relevant for the RF-properties, the depth of the
recessed cap
. Second, and
especially relevant for the RF-properties, the depth of the
recessed cap
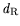 (see Fig. 7.23), in combination with
the available cap doping, determines the current path in the
barrier layer and thus the source resistance
(see Fig. 7.23), in combination with
the available cap doping, determines the current path in the
barrier layer and thus the source resistance
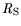 . Since the
current path is involved, this again depends on the source side
ohmic contacting, see Fig. 3.25.
The SRH generation/recombination significantly changes when
increasing
. Since the
current path is involved, this again depends on the source side
ohmic contacting, see Fig. 3.25.
The SRH generation/recombination significantly changes when
increasing
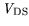 between 0.5
between 0.5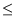
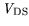
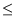 2 V. This is due
to the fact, that the shape of the space charge region changes in
the bias range 0.5 V
2 V. This is due
to the fact, that the shape of the space charge region changes in
the bias range 0.5 V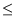
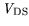
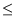 1.5 V for constant
1.5 V for constant
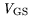 . The pronounced non-symmetric shape of the space charge
region under the gate for normal operation develops, since
normally
. The pronounced non-symmetric shape of the space charge
region under the gate for normal operation develops, since
normally
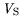 = 0
= 0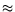
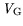
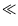
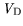 .
Impact ionization in the InAlAs/InGaAs device influences changes the output conductance by the
following factors: an additional contribution is added to the drain current
.
Impact ionization in the InAlAs/InGaAs device influences changes the output conductance by the
following factors: an additional contribution is added to the drain current
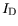 due to increase
electron concentration. However, this contribution is small for the typical region
due to increase
electron concentration. However, this contribution is small for the typical region 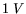
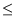
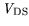
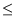
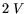 . The generation of holes to enhance the gate-current
. The generation of holes to enhance the gate-current
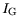 and to cause an
effective potential change near the gate is much more significant. This potential shift acts like a
and to cause an
effective potential change near the gate is much more significant. This potential shift acts like a
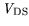 dependent positive shift of the gate potential and, once the accumulation of holes at the
source rises, leads to relatively stronger shifts of the output conductance
dependent positive shift of the gate potential and, once the accumulation of holes at the
source rises, leads to relatively stronger shifts of the output conductance
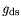 resulting e.g.
in ''kinks''. An increase of impact ionization due to increased self-heating for channel materials
with high In content is a secondary effect for higher
resulting e.g.
in ''kinks''. An increase of impact ionization due to increased self-heating for channel materials
with high In content is a secondary effect for higher
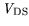 bias.
Fig. 7.37 shows the input characteristics for the
bias.
Fig. 7.37 shows the input characteristics for the
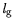 = 150 nm device with the
parameter
= 150 nm device with the
parameter
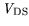 . A strong increase can be observed leading to the well known bell shaped curve.
The gate currents are influenced by direct/SRH generation/recombination and by impact ionization.
Already the non impact ionization generation processes (due to the direct band gap of
InAlAs/InGaAs) do significantly influence the gate currents. Actually, due to the space charge
region at the gate, for a detailed analysis, all generation/recombination processes must be
considered. In a HEMT biased at
. A strong increase can be observed leading to the well known bell shaped curve.
The gate currents are influenced by direct/SRH generation/recombination and by impact ionization.
Already the non impact ionization generation processes (due to the direct band gap of
InAlAs/InGaAs) do significantly influence the gate currents. Actually, due to the space charge
region at the gate, for a detailed analysis, all generation/recombination processes must be
considered. In a HEMT biased at
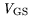 at
at
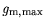 , depleted regions (barrier- SRH, direct
recombination) are adjacent to highly doped region (semiconductor caps- Auger) and regions with
high carrier concentrations and current flow (channel - Auger, impact ionization). As AlGaAs,
InAlAs, and InGaAs are direct semiconductors for typical material compositions used in HEMTs,
direct processes are considered. Fig. 7.37 and Fig. 7.38 show, that using the models
presented in Chapter 3, the gate currents can be reproduced.
Fig. 7.38 shows the simulated and measured input characteristics as a function of
temperature. The gate current
, depleted regions (barrier- SRH, direct
recombination) are adjacent to highly doped region (semiconductor caps- Auger) and regions with
high carrier concentrations and current flow (channel - Auger, impact ionization). As AlGaAs,
InAlAs, and InGaAs are direct semiconductors for typical material compositions used in HEMTs,
direct processes are considered. Fig. 7.37 and Fig. 7.38 show, that using the models
presented in Chapter 3, the gate currents can be reproduced.
Fig. 7.38 shows the simulated and measured input characteristics as a function of
temperature. The gate current
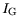 increases with increasing substrate temperature
increases with increasing substrate temperature
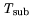 for
these devices, which is typical for an In content
for
these devices, which is typical for an In content 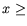 0.53. The reason is the positive
coefficient of the impact ionization, which was discussed in Chapter 3 and Chapter 6, respectively.
Fig. 7.39 shows the simulated and measured
S-parameters of the InP HEMT between 2 GHz and 120 GHz. Parasitic
elements have been obtained by the same procedure as for GaAs
devices. Good agreement is found based on the eight-element
circuit presented in Fig. 4.1. The additional elements
presented in Fig. 4.2 are not accounted for in this low
bias
0.53. The reason is the positive
coefficient of the impact ionization, which was discussed in Chapter 3 and Chapter 6, respectively.
Fig. 7.39 shows the simulated and measured
S-parameters of the InP HEMT between 2 GHz and 120 GHz. Parasitic
elements have been obtained by the same procedure as for GaAs
devices. Good agreement is found based on the eight-element
circuit presented in Fig. 4.1. The additional elements
presented in Fig. 4.2 are not accounted for in this low
bias
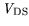 = 1 V case, where high field effects do not dominate
the S-parameters.
= 1 V case, where high field effects do not dominate
the S-parameters.
Figure 7.39:
Simulated (-) and measured (+)
S-parameters of a dual channel InP HEMT with 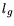 = 150 nm.
= 150 nm.
![\includegraphics[width=9 cm]{D:/Userquay/Promotion/HtmlDiss/fig62.eps}](img889.gif)
|
Fig. 7.40 shows the simulated and measured
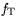 as a function of
as a function of
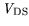 bias at
constant
bias at
constant
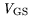 . A strong decrease of
. A strong decrease of
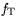 can be seen, which is based on three factors of
influence. The increasing gate currents
can be seen, which is based on three factors of
influence. The increasing gate currents
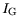 shown in Fig. 7.37 decrease the current gain
shown in Fig. 7.37 decrease the current gain
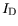 /
/
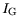 . Second,
. Second,
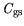 increases due to the occurrence of RST, i.e., electrons leave the
channel into the spacer and barrier. Thus, the center of the channel charge moves closer to the
gate, which leads to an increase of
increases due to the occurrence of RST, i.e., electrons leave the
channel into the spacer and barrier. Thus, the center of the channel charge moves closer to the
gate, which leads to an increase of
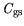 .
A third factor is the change of generation/recombination with rising
.
A third factor is the change of generation/recombination with rising
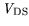 due to the
change of the extension of the space charge region. This enhances hole gate currents and leads to a
potential shift at the gate. The holes lead to an effective positive shift of
due to the
change of the extension of the space charge region. This enhances hole gate currents and leads to a
potential shift at the gate. The holes lead to an effective positive shift of
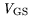 causing
higher
causing
higher
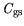 . This contributes to the observed decrease of
. This contributes to the observed decrease of
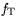 .
.


Next: 7.6.2 Technology F: Metamorphic Depletion
Up: 7.6 Technologies Based on
Previous: 7.6 Technologies Based on
Quay
2001-12-21
![]() = 150 nm
In
= 150 nm
In![]() AlAs/In
AlAs/In![]() Ga
Ga![]() As/InP device as a function
of temperature
As/InP device as a function
of temperature
![]() . For the applied
. For the applied
![]() = 0.75 V, the
device shows a DC-
= 0.75 V, the
device shows a DC-
![]() of nearly 1000 mS/mm. The transfer
characteristics further shows a decrease of
of nearly 1000 mS/mm. The transfer
characteristics further shows a decrease of
![]() and
and
![]() with rising temperature.
with rising temperature.
![]() = 300 K. For the ohmic contacts Case I in Fig. 3.25 is assumed in
the model based on geometry information. Very good agreement is found for this device between
simulation and measurements based on the model parameter values given in Chapter 3. As a basic
result, the output conductance cannot be understood without taking electrons and holes and their
generation/recombination into account. Four factors are found significant for this high
gain device and to be responsible for the output conductance in this static simulation analysis.
The transient behavior of the generation/recombination is not included.
= 300 K. For the ohmic contacts Case I in Fig. 3.25 is assumed in
the model based on geometry information. Very good agreement is found for this device between
simulation and measurements based on the model parameter values given in Chapter 3. As a basic
result, the output conductance cannot be understood without taking electrons and holes and their
generation/recombination into account. Four factors are found significant for this high
gain device and to be responsible for the output conductance in this static simulation analysis.
The transient behavior of the generation/recombination is not included.
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig60.eps}](img884.gif)
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig61.eps}](img885.gif)
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig63.eps}](img890.gif)
![]() as a function of
as a function of
![]() bias at
constant
bias at
constant
![]() . A strong decrease of
. A strong decrease of
![]() can be seen, which is based on three factors of
influence. The increasing gate currents
can be seen, which is based on three factors of
influence. The increasing gate currents
![]() shown in Fig. 7.37 decrease the current gain
shown in Fig. 7.37 decrease the current gain
![]() /
/
![]() . Second,
. Second,
![]() increases due to the occurrence of RST, i.e., electrons leave the
channel into the spacer and barrier. Thus, the center of the channel charge moves closer to the
gate, which leads to an increase of
increases due to the occurrence of RST, i.e., electrons leave the
channel into the spacer and barrier. Thus, the center of the channel charge moves closer to the
gate, which leads to an increase of
![]() .
A third factor is the change of generation/recombination with rising
.
A third factor is the change of generation/recombination with rising
![]() due to the
change of the extension of the space charge region. This enhances hole gate currents and leads to a
potential shift at the gate. The holes lead to an effective positive shift of
due to the
change of the extension of the space charge region. This enhances hole gate currents and leads to a
potential shift at the gate. The holes lead to an effective positive shift of
![]() causing
higher
causing
higher
![]() . This contributes to the observed decrease of
. This contributes to the observed decrease of
![]() .
.