2.5 Calibration of Models

Although TCAD simulation tools rely on sophisticated physical models, they need to be calibrated in order to deliver accurate results when compared to the available measurements. Once a match between measurements and simulation has been achieved, the models can be expected to represent an acceptable substitute for their real world counterparts.

However, the parameters which are incorporated in a simulation model and the conditions under which a model is operating, span huge multidimensional spaces. Therefore, it is not a trivial task to achieve an acceptable fit for each set of the model's operating conditions. Some iterative procedure is necessary to identify acceptable settings of the model parameters. The difficulty arises from the coupling between model parameters. This means that these settings cannot be determined individually while at the same time all remaining parameters are kept constant. Instead of searching for the value of each parameter individually one must rather search for an optimal set of all parameters as long as they are not independent from each other, which will rarely be the case.

Figure 2.9 depicts the basic procedure which is used to find an optimal set of model parameters.

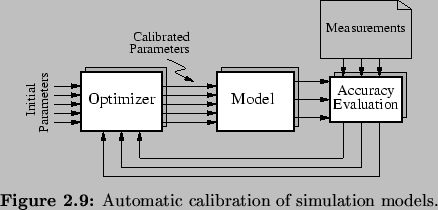
Relying on measurements, an optimizer is tuning the parameters of a model in order to obtain that set of parameters which results in a minimal overall error. This procedure includes several degrees of freedom. At first, a measure has to be defined which characterizes the error between the model's results and the corresponding measurements. Secondly, one needs to combine the results for particular operating conditions into an overall error.