Appendix A
Mathematical Tools
A.1 The Kronecker Product
For matrices 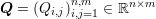 and
and 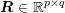 , the Kronecker product is defined as the
block matrix
, the Kronecker product is defined as the
block matrix
Q⊗R = 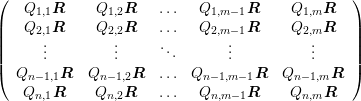 ∈ ℝnp×mq . ∈ ℝnp×mq . | | |
The Kronecker product is bilinear and associative, but not commutative. Moreover, if the
matrices 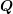 ,
, 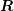 ,
, 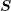 and
and 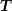 are such that the products
are such that the products 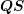 and
and 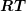 can be formed, there
holds
can be formed, there
holds
| (Q⊗R)(S ⊗T) = (QS) ⊗ (RT) . | | |
A direct consequence is that 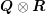 is invertible if and only if
is invertible if and only if 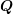 and
and 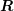 are invertible. In this
case, the inverse is given by
are invertible. In this
case, the inverse is given by
Suppose now that  and
and 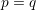 , i.e.
, i.e. 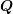 and
and 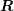 are square matrices. Let
are square matrices. Let  denote the eigenvalues of
denote the eigenvalues of 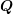 , and
, and  denote the eigenvalues of
denote the eigenvalues of 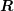 . Then the
eigenvalues of
. Then the
eigenvalues of 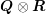 are given by
are given by
| λiμj, i = 1,…,n,j = 1,…,p . | | |
A similar statement holds true for the singular values of general rectangular matrices 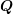 and
and
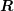 . In particular, there holds
. In particular, there holds
rank Q⊗R Q⊗R = rankQ× rankR . = rankQ× rankR . | | |
A.2 Wigner 3jm Symbols
The symbol
 with
parameters being either integers or half-integers is called a Wigner 3jm symbol arising in coupled
angular momenta between two quantum systems. It is zero unless all of the following selection
rules apply:
with
parameters being either integers or half-integers is called a Wigner 3jm symbol arising in coupled
angular momenta between two quantum systems. It is zero unless all of the following selection
rules apply:
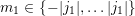 ,
, 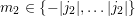 and
and 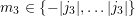 ,
,
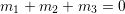 ,
,
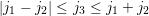 .
.
The connection with spherical harmonics is the following:
| ∫
ΩY l1,m1Y l2,m2Y l3,m3dΩ = | 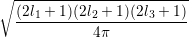 | |
|
| ×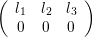 × ×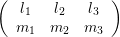 , , | | |
where the left hand side is often termed Slater integral.
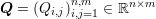 and
and 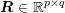 , the Kronecker product is defined as the
block matrix
, the Kronecker product is defined as the
block matrix
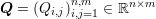 and
and 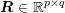 , the Kronecker product is defined as the
block matrix
, the Kronecker product is defined as the
block matrix
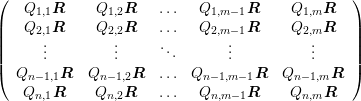 ∈ ℝnp×mq .
∈ ℝnp×mq .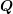 ,
, 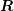 ,
, 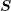 and
and 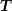 are such that the products
are such that the products 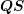 and
and 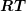 can be formed, there
holds
can be formed, there
holds
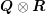 is invertible if and only if
is invertible if and only if 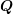 and
and 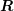 are invertible. In this
case, the inverse is given by
are invertible. In this
case, the inverse is given by
 and
and 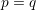 , i.e.
, i.e. 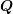 and
and 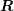 are square matrices. Let
are square matrices. Let  denote the eigenvalues of
denote the eigenvalues of 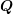 , and
, and  denote the eigenvalues of
denote the eigenvalues of 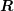 . Then the
eigenvalues of
. Then the
eigenvalues of 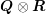 are given by
are given by
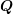 and
and
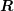 . In particular, there holds
. In particular, there holds
 Q⊗R
Q⊗R = rankQ× rankR .
= rankQ× rankR .
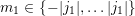 ,
, 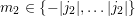 and
and 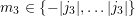 ,
,
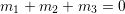 ,
,
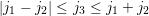 .
.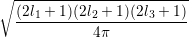
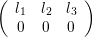 ×
×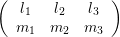 ,
,