Chapter 9
Outlook and Conclusion
Even though several improvements of the SHE method are presented throughout this thesis,
many possible further directions remain. In fact, the suggested improvements have lead to a
number of direct follow-up research topics. Consequently, a discussion of possible further
improvements on the SHE method is given in the next section. Finally, a conclusion is
drawn.
9.1 Possible Further Improvements of the SHE Method
A lexicographically ordered list of possible improvements is briefly discussed in the following. The
selection of topics is mostly based on an improvement of the method from the numerics point of
view, because the author considers the method to be more mature from the physics point of view
than from the numerics point of view.
9.1.1 Bipolar SHE
The SHE method has so far been applied to either electrons or holes, but not both.
The other carrier type has either been modelled by a continuity equation, or has been
neglected. However, a distribution function for both carrier polarities is of interest for the
investigation of high energy effects such as impact ionization feedback [54, 12], where
highly energetic carriers interact with the crystal lattice and generate electron-hole
pairs.
A challenging question is in the modeling of generation and recombination of carriers. While
for a unipolar SHE the scattering operator 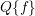 acts on a single distribution function, a bipolar
SHE requires the consideration of the distribution functions
acts on a single distribution function, a bipolar
SHE requires the consideration of the distribution functions 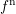 and
and 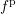 for electrons
and holes respectively, leading to a scattering operator of the form
for electrons
and holes respectively, leading to a scattering operator of the form 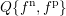 . A
Shockley-Read-Hall-like relaxation-time approach for the generation and regeneration of
carriers can serve as a first approach to modelling the interactions of electrons and holes,
but higher sophistication is expected to be required for modelling high-energy effects
accurately.
. A
Shockley-Read-Hall-like relaxation-time approach for the generation and regeneration of
carriers can serve as a first approach to modelling the interactions of electrons and holes,
but higher sophistication is expected to be required for modelling high-energy effects
accurately.
9.1.2 Energy Grid with Hanging Nodes
Due to the numerical stabilization using the 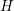 -transform discussed in Sec. 2.3, a
tensor-prolongation of the mesh in
-transform discussed in Sec. 2.3, a
tensor-prolongation of the mesh in 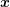 -space to the
-space to the 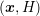 -space is attractive for the
discretization presented in Chap. 5. This prolongation for discrete total energies
-space is attractive for the
discretization presented in Chap. 5. This prolongation for discrete total energies 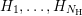 is
not fully satisfactory from the numerics point of view: The range of kinetic energies over the
device varies by an amount of
is
not fully satisfactory from the numerics point of view: The range of kinetic energies over the
device varies by an amount of  over the device, where
over the device, where  and
and 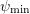 denote
the maximum and minimum of the electrostatic potential over the device. At low applied
voltages, the difference in kinetic energy ranges is about
denote
the maximum and minimum of the electrostatic potential over the device. At low applied
voltages, the difference in kinetic energy ranges is about  eV, which is certainly
acceptable. However, for higher voltages above ten Volts, as it is common for high-power
devices, the kinetic energy range consequently varies by more than ten electron volts.
This can lead to a resolution of regions of the distribution function with extremely
low probabilities of more than
eV, which is certainly
acceptable. However, for higher voltages above ten Volts, as it is common for high-power
devices, the kinetic energy range consequently varies by more than ten electron volts.
This can lead to a resolution of regions of the distribution function with extremely
low probabilities of more than 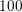 orders of magnitude below the probability near
the band edge. A resolution of these areas of extremely low probabilities is typically
not required, hence computational resources should be focused on regions with higher
importance.
orders of magnitude below the probability near
the band edge. A resolution of these areas of extremely low probabilities is typically
not required, hence computational resources should be focused on regions with higher
importance.
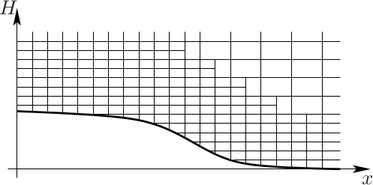
Two possible remedies for the reduction of an unnecessary high resolution at high kinetic
energies are depicted in Fig. 9.1. The first possibility is to simply truncate the simulation
domain above a certain kinetic energy and impose homogeneous Neumann boundary
conditions at the new boundaries. The truncation errors are certainly negligible if there
is no significant high-energy tail of the distribution function extending into the the
truncated region. Consequently, such a truncation is particularly interesting for larger
devices, where the mean free path of carriers is much smaller than the device dimensions.
However, for the case of small devices in the deca-nanometer regime, the high energy tail
cannot be neglected and thus a truncation of the simulation domain is inappropriate.
Nevertheless, the resolution at higher energies can be reduced by allowing so-called hanging
nodes inside the mesh. In such an approach, the energy spacing is locally increased
from 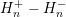 to, say,
to, say, 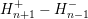 . Hanging nodes can also be introduced by
the use of nested grids, for which one may in addition decrease the spatial resolution,
cf. Fig. 9.1(b). This would further lead to the use of multigrid methods [100] for the SHE
method.
. Hanging nodes can also be introduced by
the use of nested grids, for which one may in addition decrease the spatial resolution,
cf. Fig. 9.1(b). This would further lead to the use of multigrid methods [100] for the SHE
method.
The difficulty of a mesh with hanging nodes is in the conservation of current. While the box
integration scheme in Chap. 5 asserts current conservation for sufficiently regular Delaunay
meshes by construction, it is not directly applicable for meshes with hanging nodes in
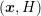 -space. On the other hand, a violation of the conservation property in low-probability
regions may be acceptable, because the error will be in the range of the machine precision due to
a violation in low-probability regions only.
-space. On the other hand, a violation of the conservation property in low-probability
regions may be acceptable, because the error will be in the range of the machine precision due to
a violation in low-probability regions only.
9.1.3 Fast Self-Consistency with Poisson’s Equation
The nonlinear coupling of the BTE with the Poisson equation requires the use of iteration
schemes as discussed in Sec. 2.4. Clearly, it is desirable to keep additional computational costs
due to these nonlinear iterations as small as possible. For simplicity, the discussion is mostly
based on uniform expansion orders, but equally applies to adaptive expansion orders presented in
Chap. 6 as well.
For a SHE method with order 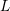 , a considerable reduction of the total simulation time can be
achieved by first computing a self-consistent solution of a first-order expansion, possibly using
a coarser grid in
, a considerable reduction of the total simulation time can be
achieved by first computing a self-consistent solution of a first-order expansion, possibly using
a coarser grid in 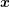 -space, larger energy spacings in
-space, larger energy spacings in 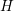 -space, or both. Since the
BTE is coupled with the Poisson equation by the carrier densities only, which in turn
depend on the zeroth-order SHE coefficient
-space, or both. Since the
BTE is coupled with the Poisson equation by the carrier densities only, which in turn
depend on the zeroth-order SHE coefficient 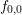 only, a first-order SHE provides a very
good initial guess for the SHE method of order
only, a first-order SHE provides a very
good initial guess for the SHE method of order 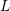 . In particular, due to the quadratic
convergence of the Newton method it is expected that a single Newton correction step
for order
. In particular, due to the quadratic
convergence of the Newton method it is expected that a single Newton correction step
for order 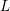 when using first-order SHE as initial guess is sufficient in most cases.
While the savings are expected to be a factor of two to three for a third-order SHE,
the savings for higher-order expansions will be roughly proportional to the number of
nonlinear iterations required for a SHE of order
when using first-order SHE as initial guess is sufficient in most cases.
While the savings are expected to be a factor of two to three for a third-order SHE,
the savings for higher-order expansions will be roughly proportional to the number of
nonlinear iterations required for a SHE of order 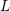 without improved initial guess for the
potential.
without improved initial guess for the
potential.
The necessity for a nonlinear iteration scheme can directly be linked with adaptive
expansion orders: As soon as the potential correction is sufficiently small, expansion orders
can be increased. This procedure can be repeated until convergence and a prescribed
accuracy is obtained. Even though the required adaptive expansion orders as well as
error indicators and adaption strategies have been proposed in this thesis, a systematic
study of the use within a nonlinear self-consistency iteration has not been carried out
yet.
9.1.4 More Flexible Discretization on Unstructured Grids
The discretization of the SHE equations on Delaunay triangulations as presented in Chap. 5
allows for a considerably better control of the local mesh size. However, the Delaunay criterion is
hard or even impossible to fulfill for mesh hierarchies often used within multilevel and multigrid
methods. As a consequence, it is desirable to employ discretization schemes suitable for arbitrary
unstructured grids.
A possible replacement for the currently employed scheme based on Voronoi diagrams is the
use of the barycenter method briefly outlined in Sec. 5.2. The discretization in Sec. 5.3 then
needs to be adjusted for the surface integral over the generalized current density 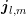 . While
each of the facets of a Voronoi box is perpendicular to the respective edge connecting two vertices,
this is not the case for the barycenter method. This leads to additional effort, because the
normal components of the fluxes with respect to the boxes are not directly available any
longer.
. While
each of the facets of a Voronoi box is perpendicular to the respective edge connecting two vertices,
this is not the case for the barycenter method. This leads to additional effort, because the
normal components of the fluxes with respect to the boxes are not directly available any
longer.
An alternative to box integration schemes are mixed finite element schemes as well as
discontinuous Galerkin methods, which have gained a lot of popularity recently [49, 85, 39].
Unlike the use of the barycenter method instead of Voronoi diagrams, a discretization for such a
case still needs to be derived. Due to the complexity of the BTE, the derivation of a suitable
formulation is expected to be considerably more involved than for well-behaved elliptic or
parabolic equations.
9.1.5 Preconditioner for the Compressed Matrix Scheme
In Chap. 4 it has been shown that the system matrix for the SHE equations can be written in the
form
 where the number of terms
where the number of terms 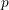 depends on the band structure model employed. The
attractiveness of this representation not only stems from the reduction of memory requirements
from
depends on the band structure model employed. The
attractiveness of this representation not only stems from the reduction of memory requirements
from 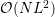 to
to 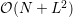 , where
, where 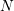 denotes the number of nodes in the
denotes the number of nodes in the 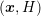 simulation domain, but also from the ability to conveniently switch between different expansion
orders. Denoting with
simulation domain, but also from the ability to conveniently switch between different expansion
orders. Denoting with 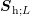 the system matrix resulting from a SHE of the BTE of order
the system matrix resulting from a SHE of the BTE of order 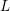 , the
system matrices for e.g.
, the
system matrices for e.g. 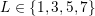 would have to be set up separately each time. With
(9.1), these system matrices are given by replacing
would have to be set up separately each time. With
(9.1), these system matrices are given by replacing 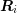 with the respective expansion
order.
with the respective expansion
order.
The main disadvantage of (9.1) are the structural restrictions during the solution phase. Since
preconditioners are required to obtain convergence of the iterative solvers, a suitable
preconditioner still needs to be found for the representation (9.1). With the availability of
adaptive expansion orders and the fact that the SHE method is basically limited by its
memory requirements rather than its computational costs, the use of uniform expansion
orders with a representation of the form (9.1) makes sense only if the preconditioner
requires memory of order 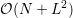 or at most
or at most 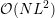 with a small factor of
proportionality in order to be comparable to the memory requirements of the
with a small factor of
proportionality in order to be comparable to the memory requirements of the 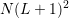 unknowns. Otherwise, the use of adaptive expansion orders is likely to be the better
choice.
unknowns. Otherwise, the use of adaptive expansion orders is likely to be the better
choice.
The preconditioner scheme discussed in Chap. 7 requires 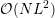 memory with a
considerably large constant of proportionality in front, which undermines the advantage
of the compressed storage of
memory with a
considerably large constant of proportionality in front, which undermines the advantage
of the compressed storage of 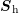 . A possibility to reduce memory requirements to
. A possibility to reduce memory requirements to
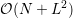 is to compute the preconditioner for first-order SHE as usual, and to define in
similarity to algebraic multigrid methods suitable transfer operators for the restriction
of the residual of the
is to compute the preconditioner for first-order SHE as usual, and to define in
similarity to algebraic multigrid methods suitable transfer operators for the restriction
of the residual of the 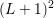 expansion coefficients to the zeroth-order expansion
coefficient, and the prolongation from the zeroth-order coefficient to the
expansion coefficients to the zeroth-order expansion
coefficient, and the prolongation from the zeroth-order coefficient to the 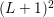 expansion coefficients. However, it is not clear whether suitable transfer operators can be
defined.
expansion coefficients. However, it is not clear whether suitable transfer operators can be
defined.
A different approach is based on an approximation on the algebraic level. Approximating first
the the system matrix 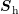 by
by
 the
preconditioner can be computed from
the
preconditioner can be computed from 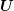 by the use of the identity
by the use of the identity 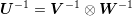 .
Consequently, only a preconditioner for
.
Consequently, only a preconditioner for 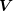 and one for
and one for 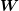 needs to be computed, which then
serves as a preconditioner for
needs to be computed, which then
serves as a preconditioner for 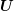 and thus for
and thus for 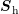 . Still, the question of whether such suitable
approximations
. Still, the question of whether such suitable
approximations 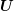 to
to 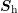 exist, is still open.
exist, is still open.
9.2 Conclusion
Throughout this thesis a number of extensions to the SHE method are proposed in order to
reduce the computational effort and consequently increase the attractiveness of the method for
every-day TCAD purposes. The suggestions enable the simulation of semiconductor
devices in the deca-nanometer regime at an unprecedented accuracy for a given time
budget.
The increased importance of hot carrier degradation in modern scaled-down devices is
addressed by proposing a scheme for the inclusion of carrier-carrier scatting for the SHE method.
Unfortunately, the scheme leads to nonlocal coupling of the equations with energy, such that
additional computational effort is required. In addition, the SHE equations become nonlinear,
which is less a concern since the SHE equations are already nonlinearly coupled with the Poisson
equation. Nevertheless, similar complications arise when considering carrier-carrier scattering with
the Monte Carlo method.
A thorough investigation of the coupling structure of the SHE equations leads to a matrix
compression scheme, which allows for storing the system matrix of the linear system of equations
after discretization in a very efficient manner. Even though the method greatly reduces memory
requirements, its use is so far hampered by the need for a suitable preconditioner for the iterative
solvers. Nevertheless, the method can already be employed in the cases where convergence is
obtained without preconditioner, and for the evaluation of residuals for adaptive expansion order
strategies.
The formulation and implementation of a higher-order discretization scheme for unstructured
grids enables the use of the SHE method as a direct replacement for established macroscopic
transport models such as the drift-diffusion model or the hydrodynamic model without changing
the underlying mesh. Moreover, the number of unknowns compared to structured grids is
reduced considerably, because refinement in unstructured grids leads to a much more
localized reduction of the mesh size than for structured grids, especially in three spatial
dimensions.
Variable-order expansions achieve the accuracy of uniform expansions at considerably lower
computational cost. The extraction of macroscopic quantities such as the carrier velocity or the
average carrier energy are shown to require only locally increased expansion orders in the
high-probability regions of the distribution function. Three different types of adaptive strategies
for the automatic choice of the expansion order are proposed.
To address the shift towards parallel computing architectures, a parallel preconditioner scheme
for the SHE method is derived based on physical principles. The resulting block-preconditioner
scheme is shown to be able to use modern multi- and many-core computing architectures such as
CPUs and GPUs efficiently. Performance gains of up to one order of magnitude compared to
single-threaded executions are obtained.
On the overall, the novel methods presented in this thesis allow for a reduction of execution
times for device simulations employing the SHE method by up to two orders of magnitude
compared to existing approaches. In addition, memory requirements are reduced by about one
order of magnitude, thus allowing for higher accuracy for a given amount of memory. The
proposed algorithms are implemented in the freely available open source device simulator
ViennaSHE.
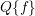 acts on a single distribution function, a bipolar
SHE requires the consideration of the distribution functions
acts on a single distribution function, a bipolar
SHE requires the consideration of the distribution functions 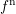 and
and 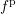 for electrons
and holes respectively, leading to a scattering operator of the form
for electrons
and holes respectively, leading to a scattering operator of the form 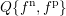 . A
Shockley-Read-Hall-like relaxation-time approach for the generation and regeneration of
carriers can serve as a first approach to modelling the interactions of electrons and holes,
but higher sophistication is expected to be required for modelling high-energy effects
accurately.
. A
Shockley-Read-Hall-like relaxation-time approach for the generation and regeneration of
carriers can serve as a first approach to modelling the interactions of electrons and holes,
but higher sophistication is expected to be required for modelling high-energy effects
accurately.
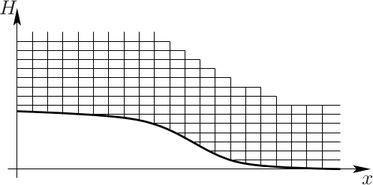
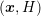 -space.
-space. -transform discussed in Sec.
-transform discussed in Sec.  -space to the
-space to the 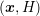 -space is attractive for the
discretization presented in Chap.
-space is attractive for the
discretization presented in Chap. 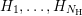 is
not fully satisfactory from the numerics point of view: The range of kinetic energies over the
device varies by an amount of
is
not fully satisfactory from the numerics point of view: The range of kinetic energies over the
device varies by an amount of  over the device, where
over the device, where  and
and 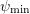 denote
the maximum and minimum of the electrostatic potential over the device. At low applied
voltages, the difference in kinetic energy ranges is about
denote
the maximum and minimum of the electrostatic potential over the device. At low applied
voltages, the difference in kinetic energy ranges is about  eV, which is certainly
acceptable. However, for higher voltages above ten Volts, as it is common for high-power
devices, the kinetic energy range consequently varies by more than ten electron volts.
This can lead to a resolution of regions of the distribution function with extremely
low probabilities of more than
eV, which is certainly
acceptable. However, for higher voltages above ten Volts, as it is common for high-power
devices, the kinetic energy range consequently varies by more than ten electron volts.
This can lead to a resolution of regions of the distribution function with extremely
low probabilities of more than 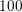 orders of magnitude below the probability near
the band edge. A resolution of these areas of extremely low probabilities is typically
not required, hence computational resources should be focused on regions with higher
importance.
orders of magnitude below the probability near
the band edge. A resolution of these areas of extremely low probabilities is typically
not required, hence computational resources should be focused on regions with higher
importance.
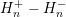 to, say,
to, say, 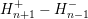 . Hanging nodes can also be introduced by
the use of nested grids, for which one may in addition decrease the spatial resolution,
cf. Fig.
. Hanging nodes can also be introduced by
the use of nested grids, for which one may in addition decrease the spatial resolution,
cf. Fig. 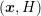 -space. On the other hand, a violation of the conservation property in low-probability
regions may be acceptable, because the error will be in the range of the machine precision due to
a violation in low-probability regions only.
-space. On the other hand, a violation of the conservation property in low-probability
regions may be acceptable, because the error will be in the range of the machine precision due to
a violation in low-probability regions only.
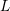 , a considerable reduction of the total simulation time can be
achieved by first computing a self-consistent solution of a first-order expansion, possibly using
a coarser grid in
, a considerable reduction of the total simulation time can be
achieved by first computing a self-consistent solution of a first-order expansion, possibly using
a coarser grid in 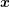 -space, larger energy spacings in
-space, larger energy spacings in 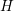 -space, or both. Since the
BTE is coupled with the Poisson equation by the carrier densities only, which in turn
depend on the zeroth-order SHE coefficient
-space, or both. Since the
BTE is coupled with the Poisson equation by the carrier densities only, which in turn
depend on the zeroth-order SHE coefficient 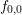 only, a first-order SHE provides a very
good initial guess for the SHE method of order
only, a first-order SHE provides a very
good initial guess for the SHE method of order 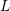 . In particular, due to the quadratic
convergence of the Newton method it is expected that a single Newton correction step
for order
. In particular, due to the quadratic
convergence of the Newton method it is expected that a single Newton correction step
for order 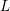 when using first-order SHE as initial guess is sufficient in most cases.
While the savings are expected to be a factor of two to three for a third-order SHE,
the savings for higher-order expansions will be roughly proportional to the number of
nonlinear iterations required for a SHE of order
when using first-order SHE as initial guess is sufficient in most cases.
While the savings are expected to be a factor of two to three for a third-order SHE,
the savings for higher-order expansions will be roughly proportional to the number of
nonlinear iterations required for a SHE of order 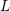 without improved initial guess for the
potential.
without improved initial guess for the
potential.
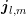 . While
each of the facets of a Voronoi box is perpendicular to the respective edge connecting two vertices,
this is not the case for the barycenter method. This leads to additional effort, because the
normal components of the fluxes with respect to the boxes are not directly available any
longer.
. While
each of the facets of a Voronoi box is perpendicular to the respective edge connecting two vertices,
this is not the case for the barycenter method. This leads to additional effort, because the
normal components of the fluxes with respect to the boxes are not directly available any
longer.

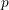 depends on the band structure model employed. The
attractiveness of this representation not only stems from the reduction of memory requirements
from
depends on the band structure model employed. The
attractiveness of this representation not only stems from the reduction of memory requirements
from 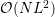 to
to 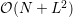 , where
, where 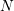 denotes the number of nodes in the
denotes the number of nodes in the 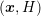 simulation domain, but also from the ability to conveniently switch between different expansion
orders. Denoting with
simulation domain, but also from the ability to conveniently switch between different expansion
orders. Denoting with 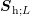 the system matrix resulting from a SHE of the BTE of order
the system matrix resulting from a SHE of the BTE of order 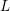 , the
system matrices for e.g.
, the
system matrices for e.g. 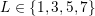 would have to be set up separately each time. With
(9.1), these system matrices are given by replacing
would have to be set up separately each time. With
(9.1), these system matrices are given by replacing 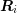 with the respective expansion
order.
with the respective expansion
order.
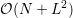 or at most
or at most 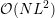 with a small factor of
proportionality in order to be comparable to the memory requirements of the
with a small factor of
proportionality in order to be comparable to the memory requirements of the 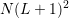 unknowns. Otherwise, the use of adaptive expansion orders is likely to be the better
choice.
unknowns. Otherwise, the use of adaptive expansion orders is likely to be the better
choice.
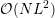 memory with a
considerably large constant of proportionality in front, which undermines the advantage
of the compressed storage of
memory with a
considerably large constant of proportionality in front, which undermines the advantage
of the compressed storage of 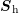 . A possibility to reduce memory requirements to
. A possibility to reduce memory requirements to
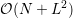 is to compute the preconditioner for first-order SHE as usual, and to define in
similarity to algebraic multigrid methods suitable transfer operators for the restriction
of the residual of the
is to compute the preconditioner for first-order SHE as usual, and to define in
similarity to algebraic multigrid methods suitable transfer operators for the restriction
of the residual of the 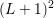 expansion coefficients to the zeroth-order expansion
coefficient, and the prolongation from the zeroth-order coefficient to the
expansion coefficients to the zeroth-order expansion
coefficient, and the prolongation from the zeroth-order coefficient to the 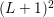 expansion coefficients. However, it is not clear whether suitable transfer operators can be
defined.
expansion coefficients. However, it is not clear whether suitable transfer operators can be
defined.
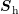 by
by

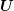 by the use of the identity
by the use of the identity 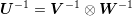 .
Consequently, only a preconditioner for
.
Consequently, only a preconditioner for 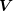 and one for
and one for 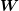 needs to be computed, which then
serves as a preconditioner for
needs to be computed, which then
serves as a preconditioner for 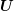 and thus for
and thus for 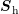 . Still, the question of whether such suitable
approximations
. Still, the question of whether such suitable
approximations 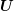 to
to 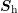 exist, is still open.
exist, is still open.