

Next: 2.2 Leitungswiderstand
Up: 2. Grundlagen
Previous: 2. Grundlagen
Unterabschnitte
Für den stationären Fall mit linearer Dielektrizitätszahl ist das
Verhältnis von Ladung 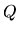 und Spannung
und Spannung 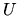 zweier voneinander isolierter
Leiter konstant und wird als Kapazität
zweier voneinander isolierter
Leiter konstant und wird als Kapazität 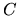 bezeichnet
bezeichnet
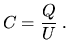 |
(2.11) |
Da die Leiter im Inneren feldfrei sind, ist das Potenzial dort konstant und die
Ladung ist ausschließlich auf der Oberfläche der Leiter verteilt.
Die Ladungsverteilung ergibt sich aus der elektrischen Flussdichte
 gemäß der dritten Maxwell'schen Gleichung (2.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit der
Dicke
gemäß der dritten Maxwell'schen Gleichung (2.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit der
Dicke  und lässt
und lässt 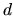 gegen Null gehen, so erhält man die
Flächenladungsdichte
gegen Null gehen, so erhält man die
Flächenladungsdichte 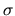 als Differenz der Normalkomponenten von
als Differenz der Normalkomponenten von
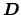 außerhalb (
außerhalb (
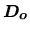 ) und innerhalb (
) und innerhalb (
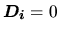 ) des Leiters
) des Leiters
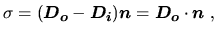 |
(2.12) |
wobei der Vektor
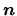 normal auf die Leiteroberfläche steht und in
Richtung Dielektrikum zeigt.
Mittels Ladungsintegration über die
Leiteroberfläche
normal auf die Leiteroberfläche steht und in
Richtung Dielektrikum zeigt.
Mittels Ladungsintegration über die
Leiteroberfläche 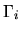
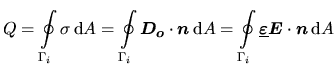 |
(2.13) |
kann man die gesamte auf einem Leiter gespeicherte Ladung berechnen.
Über (2.11) lässt sich daraus
die Kapazität zwischen zwei Leitern ermitteln.2.1
Als Alternative zur Ladungsintegration kann die Kapazität auch mit der
Energiemethode ermittelt werden.
Die in einem Kondensator gespeicherte Energie 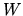 lässt sich durch
lässt sich durch
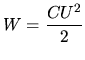 |
(2.14) |
ausdrücken, die natürlich gleich der im elektrischen Feld enthaltenen
Energie
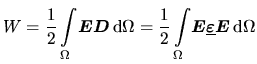 |
(2.15) |
sein muss.
Der Integrationsbereich 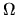 erstreckt sich über das gesamte Dielektrikum
zwischen den Leitern und geht theoretisch bis ins Unendliche.
Das elektrische Feld ladungsbalancierter Leiter klingt für Entfernungen,
die groß sind gegenüber dem Durchmesser des Gebietes,
das die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte
Teil der Feldenergie in der nächsten Umgebung der Leiter enthalten und
der Integrationsbereich kann für praktische Anwendungen entsprechend
verkleinert werden, ohne einen großen Fehler bei der Energieberechnung
zu machen.
In Abb. 2.1 ist grafisch dargestellt wie der Fehler der berechneten
Kapazität in einem zweidimensionalen Beispiel von der Größe des
Simulationsbereiches abhängig ist.
erstreckt sich über das gesamte Dielektrikum
zwischen den Leitern und geht theoretisch bis ins Unendliche.
Das elektrische Feld ladungsbalancierter Leiter klingt für Entfernungen,
die groß sind gegenüber dem Durchmesser des Gebietes,
das die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte
Teil der Feldenergie in der nächsten Umgebung der Leiter enthalten und
der Integrationsbereich kann für praktische Anwendungen entsprechend
verkleinert werden, ohne einen großen Fehler bei der Energieberechnung
zu machen.
In Abb. 2.1 ist grafisch dargestellt wie der Fehler der berechneten
Kapazität in einem zweidimensionalen Beispiel von der Größe des
Simulationsbereiches abhängig ist.
Abbildung 2.1:
Auswirkung der Größe des
Simulationsbereiches 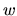 auf den Fehler
auf den Fehler 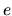 der berechneten Kapazität
in einem zweidimensionalen Beispiel
der berechneten Kapazität
in einem zweidimensionalen Beispiel
|
|
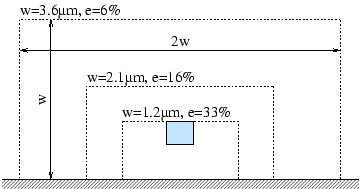
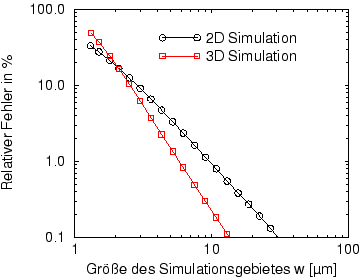
Abbildung 2.2 vergleicht den zwei- und den dreidimensionalen Fall.
Das dreidimensionale Beispiel ist im Querschnitt mit dem zweidimensionalen
ident,
und die Länge des Leiters entspricht seiner Breite.
Man erkennt, dass im zweidimensionalen Fall der Fehler der berechneten
Kapazität quadratisch gegen Null geht,
während im dreidimensionalen Fall eine Konvergenz mit der dritten Potenz
von 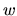 beobachtbar ist.
beobachtbar ist.
Abbildung 2.2:
Vergleich der relativen Fehler, die durch
die Einschränkung des Simulationsbereiches entstehen, im zwei- und
im dreidimensionalen Fall:
Man erkennt, dass im zweidimensionalen Fall der Fehler quadratisch und
im dreidimensionalen Fall der Fehler mit der dritten Potenz gegen Null geht.
|
|
Sowohl die Energiemethode als auch das Verfahren der Ladungsintegration
erfordern die numerische Berechnung des elektrischen Feldes.
Anzumerken ist, dass bei der Ladungsintegration die Berechnung des Feldes
auf der Leiteroberfläche ausreichend ist.
Setzt man (2.10) in (2.3) ein und berücksichtigt, dass in den
Isolatoren keine elektrischen Ladungen vorhanden sind (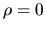 ) erhält man
die Euler-Gleichung
) erhält man
die Euler-Gleichung
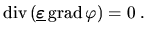 |
(2.16) |
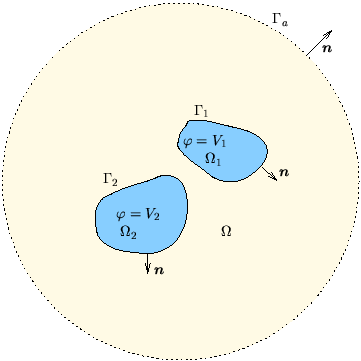
Das Gebiet 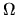 , auf dem Gleichung (2.16) gelöst werden soll wird
durch mehrere Flächen berandet (Abb. 2.3).
, auf dem Gleichung (2.16) gelöst werden soll wird
durch mehrere Flächen berandet (Abb. 2.3).
Abbildung 2.3:
Simulationsbereich und Ränder
bei der Berechnung des elektrischen Feldes:
Die beiden Elektroden 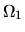 und
und 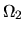 liegen auf konstanten
Potenzialen (
liegen auf konstanten
Potenzialen (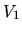 bzw.
bzw. 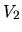 ) und bilden somit
Dirichlet-Bedingungen.
Der äußere Rand (punktierte Linie) wird durch eine homogene
Neumann-Bedingung modelliert.
) und bilden somit
Dirichlet-Bedingungen.
Der äußere Rand (punktierte Linie) wird durch eine homogene
Neumann-Bedingung modelliert.
|
|
Die konstanten Potenziale der Leiteroberflächen stellen
Dirichlet-Bedingungen dar
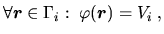 |
(2.17) |
wobei mit 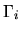 die Oberfläche des Leiters
die Oberfläche des Leiters 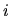 bezeichnet wird.
Wenn man für die numerische Berechnung das Simulationsgebiet nach außen hin
begrenzt, benötigt man auch für
bezeichnet wird.
Wenn man für die numerische Berechnung das Simulationsgebiet nach außen hin
begrenzt, benötigt man auch für 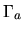 eine Randbedingung, die
man sinnvollerweise so wählt, dass die Oberfläche ladungsfrei bleibt,
also
eine Randbedingung, die
man sinnvollerweise so wählt, dass die Oberfläche ladungsfrei bleibt,
also
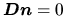 gilt, oder durch das Potenzial ausgedrückt:
gilt, oder durch das Potenzial ausgedrückt:
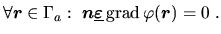 |
(2.18) |
Diese Art von Randbedingung wird homogene Neumann-Bedingung genannt.
Oberflächen, auf denen eine fixe elektrische Flächenladungsdichte 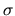 eingeprägt ist, lassen
sich durch allgemeine Neumann-Bedingungen darstellen:
eingeprägt ist, lassen
sich durch allgemeine Neumann-Bedingungen darstellen:
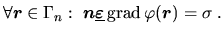 |
(2.19) |
Eine spezielle Art von Randbedingung wird für den Fall benötigt, wenn
sich im Dielektrikum zwischen den beiden Leitern, deren Kapazität berechnet
werden soll, ein weiterer leitender Körper befindet, der nicht mittels
einer Dirichlet-Bedingung auf ein fixes Potenzial gelegt werden soll.
Da hier wie in jedem Leiter
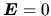 gilt, muss zwar das Potenzial auf der
gesamten Oberfläche des Leiters
gilt, muss zwar das Potenzial auf der
gesamten Oberfläche des Leiters
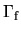 gleich groß sein, es wird aber
mit einem noch unbekannten Wert
gleich groß sein, es wird aber
mit einem noch unbekannten Wert
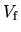 angenommen:
angenommen:
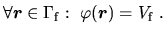 |
(2.20) |
Da dieser Leiter über keine elektrischen Anschlüsse verfügt, können
Ladungen auf der Oberfläche rein durch Influenz entstehen und müssen
in Summe Null ergeben:
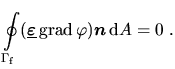 |
(2.21) |
Dieser Typ von Randbedingung wird schwebende Randbedingung
(Floating Boundary) genannt.
Bisher wurden zur Kapazitätsberechnung immer nur Zweileitersysteme
herangezogen.
Geht man jedoch von 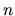 Leitern aus, so kann man von jedem Leiter
zu jedem anderen eine Kapazität definieren, man erhält also insgesamt
Leitern aus, so kann man von jedem Leiter
zu jedem anderen eine Kapazität definieren, man erhält also insgesamt
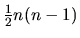 Teilkapazitäten (siehe Beispiel in Abb. 2.4).
Teilkapazitäten (siehe Beispiel in Abb. 2.4).
Abbildung 2.4:
Zehn Teilkapazitäten in einem
5-Leiter Problem
|
|
Für eine bestimmte Konfiguration von Potenzialen auf den einzelnen Leitern
(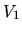 ,
, 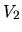 , ...
, ...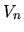 ) kann man die Gesamtenergie als Summe der
einzelnen Energien in den
) kann man die Gesamtenergie als Summe der
einzelnen Energien in den
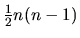 Teilkapazitäten anschreiben:
Teilkapazitäten anschreiben:
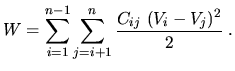 |
(2.22) |
Man erhält also eine Gleichung mit
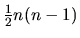 Unbekannten.
Da für eine Lösung
Unbekannten.
Da für eine Lösung
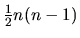 Gleichungen benötigt werden, berechnet
man die Gesamtenergie für
Gleichungen benötigt werden, berechnet
man die Gesamtenergie für
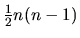 verschiedene
Potenzialkonfigurationen der Leiter.
Aus dem entstandenem linearen System lassen sich dann die Teilkapazitäten
bestimmen.
verschiedene
Potenzialkonfigurationen der Leiter.
Aus dem entstandenem linearen System lassen sich dann die Teilkapazitäten
bestimmen.
Fußnoten
- ... ermitteln.2.1
- Ein
ladungsbalanciertes System sei vorausgesetzt.



Next: 2.2 Leitungswiderstand
Up: 2. Grundlagen
Previous: 2. Grundlagen
R. Sabelka: Dreidimensionale Finite Elemente Simulation von Verdrahtungsstrukturen auf Integrierten Schaltungen
![]() und Spannung
und Spannung ![]() zweier voneinander isolierter
Leiter konstant und wird als Kapazität
zweier voneinander isolierter
Leiter konstant und wird als Kapazität ![]() bezeichnet
bezeichnet
![]() gemäß der dritten Maxwell'schen Gleichung (2.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit der
Dicke
gemäß der dritten Maxwell'schen Gleichung (2.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit der
Dicke ![]() und lässt
und lässt ![]() gegen Null gehen, so erhält man die
Flächenladungsdichte
gegen Null gehen, so erhält man die
Flächenladungsdichte ![]() als Differenz der Normalkomponenten von
als Differenz der Normalkomponenten von
![]() außerhalb (
außerhalb (
![]() ) und innerhalb (
) und innerhalb (
![]() ) des Leiters
) des Leiters
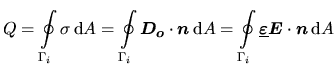
![]() lässt sich durch
lässt sich durch
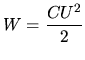
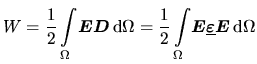
![]() beobachtbar ist.
beobachtbar ist.
![]() ) erhält man
die Euler-Gleichung
) erhält man
die Euler-Gleichung
![]() , auf dem Gleichung (2.16) gelöst werden soll wird
durch mehrere Flächen berandet (Abb. 2.3).
, auf dem Gleichung (2.16) gelöst werden soll wird
durch mehrere Flächen berandet (Abb. 2.3).
![]() gilt, muss zwar das Potenzial auf der
gesamten Oberfläche des Leiters
gilt, muss zwar das Potenzial auf der
gesamten Oberfläche des Leiters
![]() gleich groß sein, es wird aber
mit einem noch unbekannten Wert
gleich groß sein, es wird aber
mit einem noch unbekannten Wert
![]() angenommen:
angenommen:
![]() Leitern aus, so kann man von jedem Leiter
zu jedem anderen eine Kapazität definieren, man erhält also insgesamt
Leitern aus, so kann man von jedem Leiter
zu jedem anderen eine Kapazität definieren, man erhält also insgesamt
![]() Teilkapazitäten (siehe Beispiel in Abb. 2.4).
Teilkapazitäten (siehe Beispiel in Abb. 2.4).
![]() ,
, ![]() , ...
, ...![]() ) kann man die Gesamtenergie als Summe der
einzelnen Energien in den
) kann man die Gesamtenergie als Summe der
einzelnen Energien in den
![]() Teilkapazitäten anschreiben:
Teilkapazitäten anschreiben: