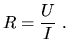 |
(2.23) |
Gemäß dem Ohm'schen Gesetz ist der elektrische Widerstand eines Leiters als das Verhältnis von Klemmenspannung und Strom definiert:
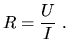 |
(2.23) |
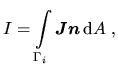 |
(2.24) |
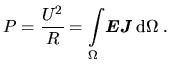 |
(2.25) |
Für die Berechnung des elektrischen Feldes geht man wieder
vom zeitlich unveränderlichen Fall aus
und nimmt die elektrische Feldstärke als reines Gradientenfeld gemäß
(2.10) an.
Ferner lässt sich zeigen, dass die Stromdichte
![]() quellenfrei ist,
indem man den Divergenzoperator auf (2.8) anwendet:
quellenfrei ist,
indem man den Divergenzoperator auf (2.8) anwendet:
| (2.26) |
Der Bereich ![]() , auf dem (2.27) gelöst werden soll,
entspricht dem Inneren des stromführenden Leiters.
Der Teil der Oberfläche, der ausschließlich von Isolatoren umgeben ist und
keine Kontakte enthält (
, auf dem (2.27) gelöst werden soll,
entspricht dem Inneren des stromführenden Leiters.
Der Teil der Oberfläche, der ausschließlich von Isolatoren umgeben ist und
keine Kontakte enthält (![]() ), stellt für das Potenzial eine
homogene Neumann-Bedingung dar, da kein Strom vom Leiter in
den Isolator fließen kann (
), stellt für das Potenzial eine
homogene Neumann-Bedingung dar, da kein Strom vom Leiter in
den Isolator fließen kann (
![]() ), und somit gilt:
), und somit gilt:
An den Kontaktflächen ![]() wird üblicherweise ein konstantes
Potenzial
wird üblicherweise ein konstantes
Potenzial ![]() vorgegeben, was eine Dirichlet-Bedingung
darstellt:
vorgegeben, was eine Dirichlet-Bedingung
darstellt:
Alternativ zu einem konstanten Potenzial könnte man auch an den Kontakten
eine konstante Stromdichte ![]() (normal zur Oberfläche) einprägen
(inhomogene Neumann-Bedingung)
(normal zur Oberfläche) einprägen
(inhomogene Neumann-Bedingung)
Wenn man hingegen anstatt der Stromdichteverteilung den Gesamtstrom
![]() angeben möchte und gleichzeitig ein konstantes Potenzial mit einem noch
unbekannten Wert
angeben möchte und gleichzeitig ein konstantes Potenzial mit einem noch
unbekannten Wert
![]() fordert,
ergibt das eine schwebende Randbedingung
fordert,
ergibt das eine schwebende Randbedingung
Wenn das Gebiet ![]() ausschließlich von Neumann-Bedingungen oder
schwebenden Randbedingungen umgeben ist,
dann hat (2.27) keine eindeutige
Lösung für das Potenzial.
Durch die Wahl eines beliebigen Potenzialwertes in einem beliebigen
Punkt
ausschließlich von Neumann-Bedingungen oder
schwebenden Randbedingungen umgeben ist,
dann hat (2.27) keine eindeutige
Lösung für das Potenzial.
Durch die Wahl eines beliebigen Potenzialwertes in einem beliebigen
Punkt
![]() kann die Eindeutigkeit wieder hergestellt werden
kann die Eindeutigkeit wieder hergestellt werden
| (2.33) |
Die folgende globale Verträglichkeitsbedingung muß immer erfüllt sein
Wenn ein Leiter mehr als nur zwei Kontakte aufweist, kann man ähnlich wie zuvor bei den Teilkapazitäten Teilwiderstände definieren (Abb. 2.5).
Für die Berechnung der
![]() Teilwiderstände, die von
Teilwiderstände, die von ![]() Kontakten
gebildet werden, benötigt man die Leistungen
Kontakten
gebildet werden, benötigt man die Leistungen ![]() für
für
![]() verschiedene Konfigurationen von Kontaktpotenzialen, um aus einem linearen
System von
verschiedene Konfigurationen von Kontaktpotenzialen, um aus einem linearen
System von
![]() Gleichungen der Form
Gleichungen der Form
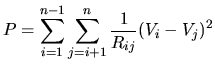 |
(2.35) |