The model function is based on a physically motivated interpolation of the terminal currents and charges of the device. The interpolation also supplies the derivatives, i.e., the conductance and capacitance matrices of the device. These data are directly interfaced to a new circuit simulator, MINISIM [73], which uses charge conservative capacitance modeling. This approach rules out common problems like, e.g., discrepancies between the AC-model conductance parameters and the derivatives of the DC-model currents.
The interpolation uses piecewise polynomial and/or exponential
splines in each dimension (e.g.,
![]() ,
,
![]() :
polynomial;
:
polynomial;
![]() :
exponential) to account for the physical nature of the
quantities (especially the exponential dependence of the currents).
The interpolation functions have the following form:
:
exponential) to account for the physical nature of the
quantities (especially the exponential dependence of the currents).
The interpolation functions have the following form:
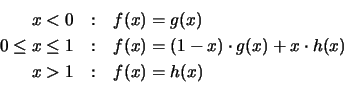 |
(4.3) |
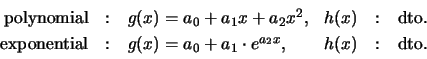 |
(4.4) |
![\includegraphics[scale=1.2]{intfunc.eps}](img528.gif)
|
To determine the accuracy of the model (4.5) was
used as a test function (cf. the EKV model [42]).
The worst-case interpolation error,
i.e., the ![]() norm of the relative error,
was determined numerically as a function of the gate voltage
(cf. Fig. 4.6). The modified exponential interpolation
is clearly better than the cubic one, yielding an error
of < 0.2% for the function value and < 2.0% for the
derivative.
norm of the relative error,
was determined numerically as a function of the gate voltage
(cf. Fig. 4.6). The modified exponential interpolation
is clearly better than the cubic one, yielding an error
of < 0.2% for the function value and < 2.0% for the
derivative.
![\includegraphics[scale=1.0]{erel-x.eps}](img532.gif)
|
![\includegraphics[scale=1.0]{erel-n.eps}](img536.gif)
|
The maximum error of the output conductance go was determined
numerically, using the following test expression:
![\includegraphics[scale=1.0]{erel-x2s.eps}](img547.gif)
|
It is important to note, that, although the polynomial interpolation
used here is generally not monotonic for monotonic samples, the
maximum error of the derivatives is well below 100%.
This is due to the fact that - apart from breakdown phenomena
- terminal quantities of a MOSFET and their derivatives cannot
change arbitrarily fast with respect to the terminal voltages.
Using
(4.5) and (4.6) it can be shown
that non-monotonicity cannot occur for a sampling interval
of less than
![]() .
Monotonicity, on the other hand, still permits an error
of 100% and is therefore not sufficient for high-accuracy circuit
simulation.
.
Monotonicity, on the other hand, still permits an error
of 100% and is therefore not sufficient for high-accuracy circuit
simulation.
These one-dimensional interpolations are then combined to a two or
three-dimensional interpolation by nesting as shown in Fig. 4.10.
A full 3-dimensional interpolation requires 64 supporting data points
around the target interval.
First, the data are interpolated in bulk-direction for 16 points in the
![]() -
-
![]() plane for the given
plane for the given
![]() :
second, the data are interpolated in
drain-direction for 4 points on the
:
second, the data are interpolated in
drain-direction for 4 points on the
![]() line for the given
line for the given
![]() ;
and
last, an interpolation is performed in gate-direction for the given
;
and
last, an interpolation is performed in gate-direction for the given
![]() .
This algorithm is also employed for the computation of the derivatives.
Although the partial interpolation of derivatives is generally not
consistent with the exact computation, the relative errors were found to be
marginal (< 10-4).
The actual algorithm uses extensive precomputation of polynomial
coefficients to ensure high CPU efficiency of the program.
.
This algorithm is also employed for the computation of the derivatives.
Although the partial interpolation of derivatives is generally not
consistent with the exact computation, the relative errors were found to be
marginal (< 10-4).
The actual algorithm uses extensive precomputation of polynomial
coefficients to ensure high CPU efficiency of the program.
In the current implementation one call to the model function takes
![]() on an HP-PA 735 workstation.
The memory consumption, taking typical numbers of
5 x 20 x 20 = 2000 data points
in
on an HP-PA 735 workstation.
The memory consumption, taking typical numbers of
5 x 20 x 20 = 2000 data points
in
![]() ,
,
![]() ,
and
,
and
![]() direction,
is about 80Kbytes per transistor type.
Saving the precomputed coefficients and decision flags could also be stored
to speed up the execution at the expense of a higher memory consumption.
direction,
is about 80Kbytes per transistor type.
Saving the precomputed coefficients and decision flags could also be stored
to speed up the execution at the expense of a higher memory consumption.