![\includegraphics[scale=1.0]{abst-fet.eps}](img673.gif)
|
The basic idea of the field effect transistor (FET) is to control the density of mobile electric charges by means of an electric field. When the charges are induced between two electrodes they can conduct an electric current. The structure of a FET as shown in Fig. A.1 is basically a three-terminal capacitor, where one of the two plates consists of a material which is not a conductor but allows mobile charge carriers (e.g. electrons) to exist at room temperature (such a material is also referred to as semiconductor). This plate is contacted at either end so that electrons can flow from the electron source to the drain.
Normally, the mobile charge density in this plate is zero, but when a voltage
![]() is applied to the control gate (with
is applied to the control gate (with
![]() )
the vertical field
)
the vertical field
![]() in the insulator with a
permittivity of
in the insulator with a
permittivity of
![]() induces an areal
charge density
induces an areal
charge density
![]() in the lower plate, which then forms a conducting channel between
source and drain.
The threshold voltage
in the lower plate, which then forms a conducting channel between
source and drain.
The threshold voltage
![]() is caused by fixed negative charges
is caused by fixed negative charges
![]() in the lower plate:
in the lower plate:
![]() ,
where
,
where
![]() is the permittivity of the plate material.
Now, when a voltage
is the permittivity of the plate material.
Now, when a voltage
![]() is applied to the drain (with
is applied to the drain (with
![]() )
a current
)
a current
![]() will flow through the cannel, which is controlled by the
gate voltage.
To calculate this current we write the charge density and the lateral
field Ex as a function of the channel potential
will flow through the cannel, which is controlled by the
gate voltage.
To calculate this current we write the charge density and the lateral
field Ex as a function of the channel potential ![]() ,
where we
assume that the lateral field is small compared to the vertical field,
i.e.,
,
where we
assume that the lateral field is small compared to the vertical field,
i.e.,
![]() (gradual-channel approximation, GCA):
(gradual-channel approximation, GCA):
| (A.1) | |||
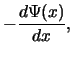 |
(A.2) |
(A.4) and (A.5) are most widely used throughout literature. Yet, whenever using these equations it should be kept in mind that they were derived from the rather simple structure in Fig. A.1, which may not reflect the physical behavior of the considered devices.