


 |  |  |
Having defined topological spaces and manifolds, which are the setting of further considerations, it is also required to define how such spaces may be combined and attached to each other. The next definitions provide the fundamentals of these endeavours and also provide the major abstraction for the storage of values in digital computers.
Definition 39 (Fibration) A continuous mapping (Definition 30)

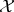 every homotopy (Definition 32)
every homotopy (Definition 32)
![f : 𝒳 × [0;1] → ℬ (4.41)](whole231x.png)

![¯
𝒳 × {0}fidX×{0}-----ℰ p (4.43)
| |
|
fF -------
𝒳 × [0;1] ℬ](whole233x.png)
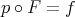 .
.
It is also commonly written as fibration sequence

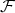 by means of a mapping into the total space
by means of a mapping into the total space
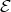 , while the second map is the fibration to the base space
, while the second map is the fibration to the base space 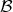 .
.
An important specialization, with an additional local requirement, can be defined which has important realizations as demonstrated in Definition 52.
Definition 40 (Fiber bundle) The topological spaces 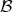 , called the base space, and
, called the base space, and 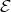 ,
called the total space, along with a surjective (Definition 23) projection (Definition 25)
,
called the total space, along with a surjective (Definition 23) projection (Definition 25)
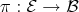 is known as a fiber bundle
is known as a fiber bundle 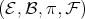 , if it locally satisfies the following condition:
, if it locally satisfies the following condition:
For every element 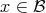 there exists an open neighbourhood
there exists an open neighbourhood 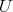 such that the preimages of the
projection
such that the preimages of the
projection 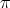 ,
, 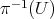 are homeomorphic to a product space
are homeomorphic to a product space 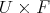 , such that the following diagram
commutes:
, such that the following diagram
commutes:
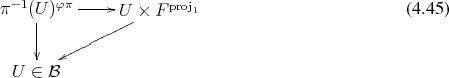
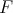 is
called a fiber over
is
called a fiber over 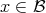 .
.
A fiber bundle is also commonly given as

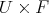 . It should not be omitted to point
out a certain kinship with Definition 35, which also features a local requirement at its core.
It is thus not surprising that manifolds can be represented as a fiber bundle, which, while
maybe not theoretically exciting, provides a guide to the storage and representation of even
non-trivial manifolds in digital form by using the fiber bundle as the main abstraction [75]. The
fiber bundle as an abstraction mechanism should not be underestimated, especially with
respect to guiding the implementations on digital computers, as the utilized memory structures
represent fiber bundles. The set of memory cells, along with a topology defined on it, acts as a
base space, on which the fiber space of values is attatched to. Fiber bundles, however, also
provide elegant and powerful solutions in the theoretical setting. Several topics covered in
Section 4.6.4 have a simple representation using fiber bundles, when also considering the following
definition.
. It should not be omitted to point
out a certain kinship with Definition 35, which also features a local requirement at its core.
It is thus not surprising that manifolds can be represented as a fiber bundle, which, while
maybe not theoretically exciting, provides a guide to the storage and representation of even
non-trivial manifolds in digital form by using the fiber bundle as the main abstraction [75]. The
fiber bundle as an abstraction mechanism should not be underestimated, especially with
respect to guiding the implementations on digital computers, as the utilized memory structures
represent fiber bundles. The set of memory cells, along with a topology defined on it, acts as a
base space, on which the fiber space of values is attatched to. Fiber bundles, however, also
provide elegant and powerful solutions in the theoretical setting. Several topics covered in
Section 4.6.4 have a simple representation using fiber bundles, when also considering the following
definition.
Beside the already presented mechanisms it is also desirable to firmly establish a formal manner in which to transport properties of mappings to various topological spaces, where they have previously not been defined. To provide Definition 44 with in depth backing, first very general notions are introduced.
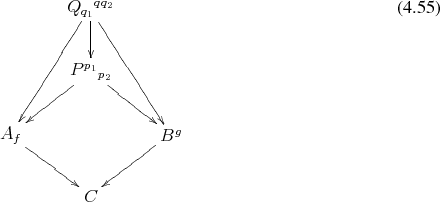
Definition 42 (Fiber product) Given two mappings with identical codomain
the fiber product over 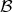 consists of two mappings
consists of two mappings
such that 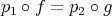 , which may also be expressed by saying that the following diagram
commutes:
, which may also be expressed by saying that the following diagram
commutes:


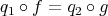 , defines a mapping
, defines a mapping

This demand ensures that a tuple 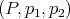 is defined uniquely up to an isomorphism. It is also
common to find the notation
is defined uniquely up to an isomorphism. It is also
common to find the notation

The general notion just defined can be applied to fiber bundles to attach fibers originally situated in one topological space to another one using a simple mapping. The formalization of this is presented next.
Definition 43 (Pullback bundle) Given a fiber bundle 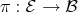 and a mapping
and a mapping 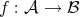 it is
possible to define a fiberbundle, the so called pullback bundle
it is
possible to define a fiberbundle, the so called pullback bundle 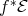 , which uses
, which uses 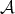 as a base space by
attaching at every element
as a base space by
attaching at every element 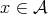 the fiber corresponding to the element
the fiber corresponding to the element 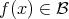 (the position of
attachment is given by the index):
(the position of
attachment is given by the index):


In short, the pullback bundle, as sketched in Figure 4.2, is simply the fiber product (Definition 42)
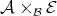 . It should not go unnoticed that this construct is compatible with sections of fiber bundles
(Definition 41); therefore entities which appear as the section of a fiber bundle, such as presented in
Definition 61 and Definition 62, will be pulled back and appear again as sections of the pullback
bundle (Definition 43).
. It should not go unnoticed that this construct is compatible with sections of fiber bundles
(Definition 41); therefore entities which appear as the section of a fiber bundle, such as presented in
Definition 61 and Definition 62, will be pulled back and appear again as sections of the pullback
bundle (Definition 43).
Considering two topological spaces 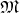 and
and 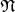 and the mappings
and the mappings

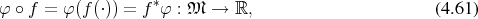
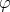 from
from 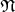 to
to 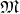 against the direction of
against the direction of 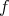 . It is said that
. It is said that
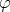 is pulled back from
is pulled back from 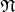 via
via 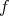 .
.
Definition 44 (Pullback (of functions)) The mapping 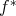 resulting from a mapping between two
topological spaces
resulting from a mapping between two
topological spaces

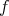 to its domain is called a pullback (of
functions).
to its domain is called a pullback (of
functions).
The pullback of functions is a particular case of the of the pullback bundle (Definition 43), which illustrates the concept in a relatively simple fashion.
 |  |  |