


 |  |  |
While the algebraic structures focus on the interplay of elements within given sets, a means to assign elements from differing sets as a special yet highly important case of Definition 4 is desired.
Definition 20 (Mapping) Considering a relation 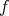 , between the sets
, between the sets 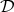 and
and 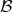 , it is
considered a map, mapping, or function, if every element of
, it is
considered a map, mapping, or function, if every element of 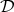 is assigned to an element of
is assigned to an element of 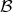 .
The converse, however, is not necessarily true that is an element of
.
The converse, however, is not necessarily true that is an element of 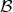 , called an image, may
result from several elements of
, called an image, may
result from several elements of 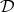 , called preimages. The set
, called preimages. The set 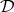 is called the domain, the set
is called the domain, the set 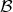 the codomain of the function
the codomain of the function 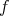 .
.
The terms mapping and function can be used synonymously.
Similar to the qualification of relations, mappings can also be further qualified. Qualifications regarding the domain and codomain are provided, from which can be deduced, if a mapping is invertible.
Definition 21 (Injective) A mapping

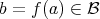 for each element
for each element 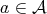 . This means that
every preimage
. This means that
every preimage 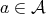 has an image
has an image 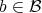 , but there may be elements in
, but there may be elements in 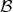 , which are not obtained
as images.
, which are not obtained
as images.
Connected to injectivity is the concept of a kernel:
Definition 22 (Kernel) For a given mapping

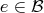 is called the kernel of the mapping
is called the kernel of the mapping
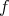
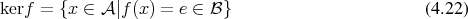
As such the kernel provides information on the injectivity of a mapping. If a mapping is injective, the kernel is trivial

Where injectivity states that there is at most one solution to every element from the domain of a function, it is also possible to assert that there is at least one image for each preimage, as is done in the next definition.
Definition 23 (Surjective) A mapping

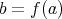 has at least one solution
has at least one solution 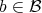 for every
for every 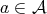 . Several
identical images in
. Several
identical images in 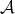 may have different preimages in
may have different preimages in 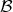 .
.
The combination of Definition 21 and Definition 23 yields:
Definition 24 (Bijective) A mapping

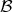 to a distinct image in
to a distinct image in
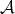 . There are no elements in
. There are no elements in 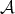 which cannot be obtained as images.
which cannot be obtained as images.
A bijective mapping, also called a bijection, is an invertible function. Since injectivity (Definition 21) demands the triviality of the kernel (Definition 22), it follows that an invertible function necessarily also has a trivial kernel.
Mappings are an essential instrument in mathematical descriptions and modelling, because it is possible to compose individual mappings in order to construct new mappings. Considering the mappings



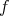 and the domain of
and the domain of 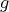 are crucial for the feasibility of such a
composition.
are crucial for the feasibility of such a
composition.
Mappings and their compositions are essential for the operation of modern computational machines, e.g., when dealing with memory management such as virtual memory, which relies on partitions as well as mappings.
The definition of cases of mappings simplifies the formulation of subsequent definitions. Therefore, several special cases are provided here in a collected form.
Definition 25 (Projection map) A projection map 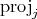 , which may also given as
, which may also given as 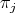 , extracts the
, extracts the 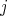 th
component of elements from a Cartesian product (Definition 3) space
th
component of elements from a Cartesian product (Definition 3) space 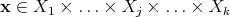 to
to 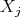 :
:

A mapping, which can be used to extend a concept from a setting to another, as is seen in Section 5.2, is provided in the following.
A subsequently important class of mappings can be abstractly described here, where realizations are then provided by Definition 70 and Definition 68.
Definition 27 (Derivation) Given an associative algebra 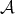 (Definition 17) and a module
(Definition 17) and a module 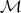 (Definition 15), a derivation is defined as a mapping
(Definition 15), a derivation is defined as a mapping
 |  |  |