


 |  |  |
Building on the available definitions, additional structures can be introduced, which can be described as being the bones of geometry as well as being useful for programming abstractions.
Definition 28 (Topology) A topology 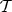 of a set
of a set 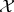 is defined by the following properties:
is defined by the following properties:
Both 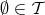 and
and 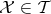 .
.
A finite intersection of members of 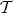 is in
is in 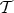 .
.
An arbitrary union of members of 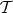 is in
is in 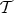 .
.
The concept of a topology alone is incomplete, when not applied to a set, thus providing:
Definition 29 (Topological space) The pair of the set 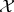 and the topology
and the topology 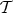 are denoted as
the topological space
are denoted as
the topological space 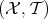 .
.
Topological spaces also allow to further qualify the concepts of mappings, as provided by Definition 20.
Definition 30 (Continuous mapping) A mapping between two topological spaces

Equipped with the concept of continuity it is beneficial to specially label a certain class of continuous, invertible mappings.
Definition 31 (Homeomorphism) A continuous mapping 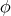 is called a homeomorphism or
topological isomorphism, if it satisfies the following properties:
is called a homeomorphism or
topological isomorphism, if it satisfies the following properties:
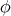 is a bijection
is a bijection
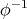 is also continuous
is also continuousBeside continuity (Definition 30), relations between two mappings from a topological space to another are of interest. Special requirements in this regard are encountered for example in Definition 39, thus motivating the following definition.
Definition 32 (Homotopy) Given two continuous mappings 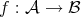 and
and 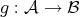 , a
homotopy
, a
homotopy 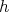 is a continuous mapping such that:
is a continuous mapping such that:
A homotopy thusly describes the smooth deformation of one mapping into another.
Further refinement of the concept of a topological space (Definition 29) by including separability of neighbourhoods of different elements of the topological space allows to move closer to the desired settings of geometry described in Definition 37.
Definition 33 (Hausdorff spaces) The topological space 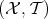 is called Hausdorff,
if
is called Hausdorff,
if

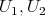 such that
such that 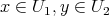 and
and 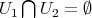 .
.
From the concept of a Hausdorff space an important definition can be derived, which is invaluable for use in the discrete settings of digital computers:
Definition 34 (CW Complex) The pair of a Hausdorff space 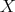 (Definition 33) together with a
decomposition
(Definition 33) together with a
decomposition 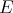 , whose elements
, whose elements 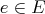 are called cells, is a CW complex, if the following criteria
are met:
are called cells, is a CW complex, if the following criteria
are met:
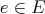 can be mapped continuously (Definition 30) to an open
ball.
can be mapped continuously (Definition 30) to an open
ball.
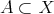 is open if and only if
is open if and only if 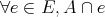 is open.
is open.A further intermediate definition is introduced, before arriving at the topological space, which carries sufficient additional structure to accommodate the geometric entities (e.g., Definition 54). It serves to again partition the requirements into manageable components, so as not to end up with overly complex and contorted constructs.
Definition 35 (Topological manifold) A topological manifold 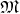 of dimension
of dimension 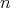 is a Hausdorff
space which is locally homeomorphic to
is a Hausdorff
space which is locally homeomorphic to 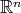 . Consequently, this results in the existence of bijective
mappings
. Consequently, this results in the existence of bijective
mappings  , called charts, of the form
, called charts, of the form

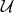 for every element
for every element 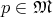 to open subsets
to open subsets 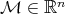 . The
. The 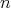 -tuple of
numbers resulting from
-tuple of
numbers resulting from 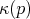 is called the (local) coordinates of
is called the (local) coordinates of 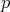 .
.
As the subsets 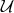 are open and the charts operate solely on them, any conclusion from a single chart
alone must remain a local one. However, open subsets may be combined to overcome this limitation
thus giving rise to:
are open and the charts operate solely on them, any conclusion from a single chart
alone must remain a local one. However, open subsets may be combined to overcome this limitation
thus giving rise to:
Definition 36 (Atlas) A collection of charts forming an open cover (Definition 1)

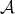 .
.
Since the atlas is now defined on the whole manifold, it is possible to judge global properties.
Considering two charts of an atlas 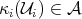 and
and 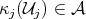 with the non-empty intersections of
open sets
with the non-empty intersections of
open sets

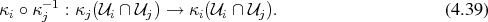
The following definition finally introduces a topological space, which is equipped to admit the differential structures required in the further geometrical considerations (Definition 48).
Definition 37 (k-Differentiable manifold) A topological manifold 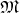 with an atlas
with an atlas 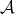 is
called a differentiable manifold, if the transitions between charts
is
called a differentiable manifold, if the transitions between charts 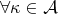 are of differentiability
class
are of differentiability
class 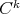 .
.
The requirement of differentiable transitions between mappings relies on the charts themselves being homeomorphisms (Definition 31) as continuity is a prerequisite for differentiability. The additional structure of a differentiable manifold also allows to place a more stringent requirement on a homeomorphism, which is expressed in the following definition.
Definition 38 (Diffeomorphism) A homeomorphism (Definition 31), which is itself differentiable as well as its inverse, is called a diffeomorphism.
Differentiable manifolds and diffeomorphisms are of particular importance for physical applications, as already attributed by the ancient adage “natura non facit saltus”.
 |  |  |