


 |  |  |
To define the distance between two objects is a concept universally graspable on an intuitive level. In mathematical terms the notion of distance as reinforced by our every day experiences can be expressed using the simple notion of an affine space (Definition 79) and the lengths of the vectors inhabiting the vector space, which is part of the affine space’s definition. This simple notion fails, however, when considering distances between geographical locations, since the shape of the world can not be modelled as an affine space, but necessarily takes the shape of a manifold (Definition 37), even if this manifold is embeddable into an affine space.
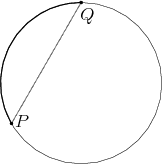
A simple example of this circumstance is presented in Figure 4.7. The manifold of a circle is embedded
in the affine space of the plane. Considering the simple case, where the circumference of a circle equals
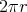 , the maximum distance between any two points on the circle is
, the maximum distance between any two points on the circle is  , while in contrast the
embedded case has a maximum distance of a mere
, while in contrast the
embedded case has a maximum distance of a mere 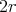 .
.
Therefore a more abstract and general approach is presented in order to alleviate this issue. Before the length can be assessed, it should be noted that the question whether any two points are connected or not, is a question of topology (Definition 28), not of the geometry built on top of this topology. The connection established by topology manifests itself in the existence of curves (Definition 45) connecting the two points under consideration. As the number of curves

 and
and 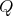 is infinite, even when the set of points involved is unique, since different
parametrization define different curves, an additional selection criterion, the length of a curve
is infinite, even when the set of points involved is unique, since different
parametrization define different curves, an additional selection criterion, the length of a curve 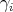 , which
is independent of the parametrization, is required to select a particular curve and assign the distance
, which
is independent of the parametrization, is required to select a particular curve and assign the distance
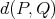 . The length of a segment of a curve may be defined using integration (Definition 95) along
the curve.
. The length of a segment of a curve may be defined using integration (Definition 95) along
the curve.
The distance is now readily obtained as the result of a minimization of the lengths of all the available
curves 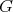 as described in Equation 4.176 connecting the desired points
as described in Equation 4.176 connecting the desired points

 is
connected to the metric tensor field (Definition 76).
is
connected to the metric tensor field (Definition 76).
 |  |  |