


 |  |  |
The integral equation under consideration in this context is the Fredholm integral equation of the second kind, which is commonly given in the form
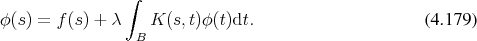
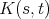 is the kernel of the integral equation. As the solution
is the kernel of the integral equation. As the solution 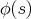 appears on both sides of
Equation 4.179, it can be inserted into itself, thus yielding
appears on both sides of
Equation 4.179, it can be inserted into itself, thus yielding
Thus the function 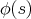 takes the form of a series
takes the form of a series
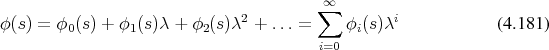
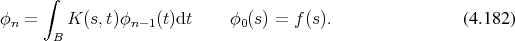
 depending only on
depending only on
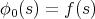 is favourable. It can be obtained by rewriting the recursion with a focus on the kernels
instead of the functions to read.
is favourable. It can be obtained by rewriting the recursion with a focus on the kernels
instead of the functions to read.

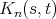 are given as
are given as
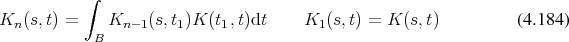
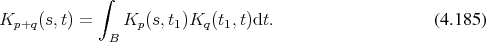
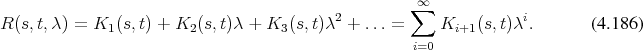
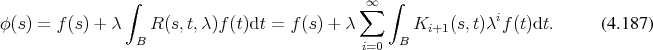
 |  |  |