


 |  |  |
While determinism was pervasive through most of the development of classical physics, it could not be maintained and uncertainty was even embraced as a central theoretical feature [79][80], as such probabilities and statistics have taken an important part among scientific modelling.
Definition 96 (Probability measure) The measure space 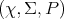 (Definition 92), where the
measure
(Definition 92), where the
measure 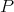 (Definition 91) has the properties
(Definition 91) has the properties
is called a probability measure. The values assigned by the measure to the subsets are called probabilities.
From the construction of probability as a measure it follows for a configuration as shown in Figure 4.8 that
which illustrates a few basic properties of probabilities which follow directly from the use of a
 -algebra (Definition 88) in the definition of a probability measure (Definition 96). The fact that the
focus is not always on the introduction of a measure on a space, but rather on the resulting structure as a
whole, warrants the following definition.
-algebra (Definition 88) in the definition of a probability measure (Definition 96). The fact that the
focus is not always on the introduction of a measure on a space, but rather on the resulting structure as a
whole, warrants the following definition.
Definition 97 (Probability space) A measure space 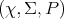 (Definition 92), where
(Definition 92), where 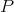 is
a probability measure (Definition 96), is called a probability space.
is
a probability measure (Definition 96), is called a probability space.
Definition 98 (Random Variable) Given a probability space 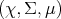 (Definition 97) and a
measurable space
(Definition 97) and a
measurable space 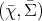 (Definition 90) a mapping of the form
(Definition 90) a mapping of the form

 -algebra
-algebra 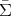 (Definition 88) are
part of the
(Definition 88) are
part of the  -algebra
-algebra 

The following definition facilitates the characterization of random variables and thus eases their handling.
Definition 99 (Probability distribution function) Given a random variable 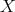 (Definition 98) joining
the probability space
(Definition 98) joining
the probability space 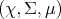 (Definition 97) and the measurable space
(Definition 97) and the measurable space 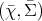 (Definition 90), it
can be used to define a mapping
(Definition 90), it
can be used to define a mapping 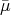 of the following form:
of the following form:
![ΣX μ -----¯Σ ¯μ (4.192)
|
|
[0;1]
¯μ = μ (X −1(b)) = μ ∘ X −1(b), ∀b ∈ ¯Σ (4.193)](whole711x.png)
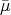 is
an induced measure on
is
an induced measure on 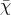 called the probability distribution function
called the probability distribution function 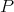 , also called the cumulative
probability function.
, also called the cumulative
probability function.
A concept closely related to the probability distribution function which allows for a local description, is given next.
Definition 100 (Probability density function) Given a probability distribution function
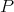 (Definition 99) the probability density function
(Definition 99) the probability density function 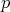 is defined as satisfying the relation
is defined as satisfying the relation
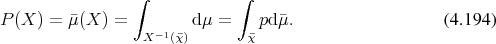
Definition 101 (Expectation value) Given a probability space 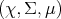 (Definition 97)
and a random variable
(Definition 97)
and a random variable 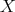 (Definition 98) the expectation value
(Definition 98) the expectation value 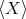 is defined by the
prescription
is defined by the
prescription

In case a probability distribution (Definition 100) is given, the expectation value also takes the shape

Among the infinite number of conceivable probability measures a few select are provided in the following, since they have uses in Section 7.2.
Definition 102 (Uniform distribution) A probability distribution 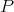 (Definition 99) on a space
(Definition 99) on a space 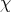 ,
which has a constant probability density function
,
which has a constant probability density function 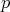 (Definition 100) is called a uniform
distribution.
(Definition 100) is called a uniform
distribution.

Definition 103 (Exponential distribution) The exponential distribution is associated to the cumulative distribution function (Definition 99).

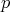 (Definition 100) can be derived to read
(Definition 100) can be derived to read

Definition 104 (Normal distribution) A probability distribution function  with a probability
density function of the shape
with a probability
density function of the shape
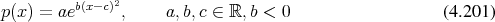
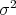 , and the mean value
, and the mean value 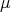 by
the expressions
by
the expressions
If this is the case and furthermore 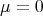 and
and 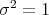 , it is commonly called standard normal
distribution.
, it is commonly called standard normal
distribution.
The importance of the normal distribution can be linked to the central limit theorem, which states that a series of independently distributed random variables approaches normal distribution in the limit and thus can be approximated using normal distribution.
The normal distribution can also be used to define other distributions as in the following.
Definition 105 (Lognormal distribution) A random variable 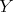 , which is obtained from a normally
distributed (Definition 104) variable
, which is obtained from a normally
distributed (Definition 104) variable 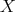 by
by

 |  |  |