


 |  |  |
Silently assuming basic familiarity with the entity known as a set [74], several distinctions connected to sets should not go undefined, especially as later concepts build on these very basic definitions and the lack of a clear distinction can be nothing but detrimental. Among others, Definition 36 is a higher level representative of the concept provided in the following definition.
Definition 1 (Open cover) An open cover 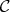 of a set
of a set 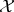 is a family of open sets
is a family of open sets 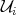 , whose union
results in
, whose union
results in 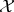 :
:

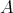 being an arbitrary index set.
being an arbitrary index set.
A similar, yet distinct concept is given in the next definition.
Definition 2 (Partition of a set) A partition of a set 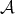 is a set
is a set 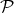 of non-empty subsets
of non-empty subsets 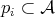 ,
which fulfil the following conditions
,
which fulfil the following conditions
Thus a partition implies that every element of the set 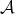 is assigned to exactly one element of the
partition
is assigned to exactly one element of the
partition 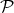 .
.
To extend the simple notion of sets and their partitions, the following definition is of high utility.
Definition 3 (Cartesian Product) The Cartesian product 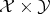 of two sets
of two sets 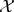 and
and 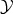 is defined
as the set of all ordered tuples of the form
is defined
as the set of all ordered tuples of the form
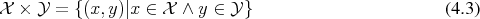
It is through this simple mechanism represented by the Cartesian product that extensions to higher dimensions are available not only in a theoretical, but especially in an applied setting.
Sets alone present elements and very basic predicates such as testing, if a given element is contained within a set. It is, however, important to provide a more involved mechanism which is readily found in relations 1 .
Definition 4 (Relation) Considering two sets 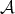 and
and 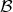 , a relation
, a relation 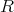 is defined as a subset of the
Cartesian product
is defined as a subset of the
Cartesian product  .
.

A relation is not only an important step for further theoretical refinement, but has also been a driving abstraction for digital data storage systems such as databases.
Relations can be further qualified with attributes in case they conform to certain requirements. A selection of qualifiers is provided in order to keep subsequent definitions from becoming unnecessarily convoluted.
Definition 5 (Reflexive relation) A binary relation 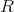 on a set
on a set 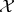 is called reflexive, if every
element is related to itself
is called reflexive, if every
element is related to itself

Definition 6 (Symmetric relation) A binary relation 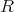 on a set
on a set 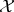 is called symmetric, if the
following is always true:
is called symmetric, if the
following is always true:
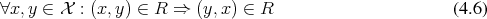
Definition 7 (Transitive relation) A binary relation 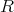 on a set
on a set 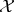 is called transitive, if it follows
that:
is called transitive, if it follows
that:
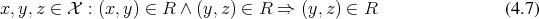
Definition 8 (Equivalence relation) A binary relation which is reflexive, transitive and symmetric is called an equivalence relation.
The application of an equivalence relation to the elements of a set leads to the concept of equivalence classes, as defined in the following.
Definition 9 (Equivalence class) Given an equivalence relation  , equivalence classes
, equivalence classes ![[x]](whole67x.png) are
defined as the sets
are
defined as the sets
![[x] = {y ∈ 𝒳 |y ∼ x } (4.8)](whole68x.png)
Equivalence classes are of special interest as they provide a means to partition a set  . The demands
placed on equivalence relations (Definition 8) ensure that a set of equivalence classes (Definition 9) is
indeed a partition of the set
. The demands
placed on equivalence relations (Definition 8) ensure that a set of equivalence classes (Definition 9) is
indeed a partition of the set  (Definition 2):
(Definition 2):
![[x ] ⁄= ∅](whole71x.png)
![[x] = [y ] ⇐ ⇒ x ∼ y](whole72x.png)
![a ∈ [x] ∧ a ∈ [y] ⇐⇒ [x] = [y].](whole73x.png)
In other words, two elements are either in the same equivalence class, or in disjoint classes. An element
![x∈[x]](whole74x.png) is called a representative of the equivalence class
is called a representative of the equivalence class ![[x]](whole75x.png) .
.
The memory within digital computers is conceptually a set, because every cell of memory can be distinctly addressed even without having to resort to querying the contents of the cells, thus it is really the structure of the cells that forms a set. The presented relations are only a small fraction of the relations available and indeed required to represent modern memory management, but are at least sufficient to cover theoretical considerations.
 |  |  |