


 |  |  |
Beside the bare structures described so far, the structures resulting from operations defined on top of the sets as a combined union gives rise to algebraic structures. They are of importance as they provide rules, how elements interacts and create new elements.
In the setting of digital computers types are models or extensions of algebraic structures. Therefore, several algebraic structures are introduced in the following with an increasing number of requirements imposed on elements and/or operations.
Definition 10 (Monoid) A set of elements 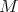 on which a binary operation
on which a binary operation 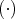 is defined is called a
monoid
is defined is called a
monoid 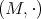 , if the binary operation satisfies the following conditions:
, if the binary operation satisfies the following conditions:
Further requirements on Definition 10 result in
Definition 11 (Group) A monoid 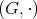 , where the binary operation additionally fulfils the condition
that for every element in
, where the binary operation additionally fulfils the condition
that for every element in 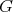 an inverse element exists, which produces the identity element under the
binary operation is called a group
an inverse element exists, which produces the identity element under the
binary operation is called a group

and as a further qualification
Definition 12 (Abelian group) When the order of the operands of the binary operation 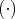 of a
group
of a
group 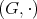 does not change its result, the group is called Abelian or commutative.
does not change its result, the group is called Abelian or commutative.

Groups are basic building blocks in the exploration of further structures, which can be defined by demanding additional operations on the basic sets.
Definition 13 (Ring) An Abelian group (Definition 12), which is equipped with an additional binary
operation under which it is a monoid (Definition 10), is called a ring 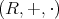 , if the two binary
relations are distributive:
, if the two binary
relations are distributive:
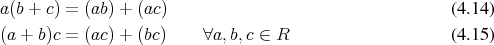
The structure of the described ring is, however, insufficient to describe the basic notion of real
numbers 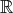 or the complex numbers
or the complex numbers 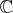 . To this end the following definition is required:
. To this end the following definition is required:
The next definition describes the algebraic structure of entities (Definition 61), which have proven to be immensely useful.
Definition 15 (Module) A Module 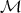 over a ring
over a ring 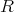 (Definition 13) is an Abelian
group (Definition 12) with respect to the operation of the addition of two elements
(Definition 13) is an Abelian
group (Definition 12) with respect to the operation of the addition of two elements 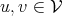 ,
while additionally being a ring with respect to the operation of multiplying elements
,
while additionally being a ring with respect to the operation of multiplying elements 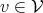 by
elements
by
elements 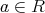 , which are called scalars.
, which are called scalars.
A related definition with somewhat stronger requirements yields a structure, which is essential for the construction of simple geometric settings.
Definition 16 (Vector space) A vector space 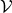 over a field
over a field 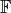 is an Abelian group with
respect to the operation of the addition of two elements
is an Abelian group with
respect to the operation of the addition of two elements 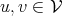 , while additionally being a
ring with respect to the operation of multiplying elements
, while additionally being a
ring with respect to the operation of multiplying elements 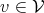 by elements
by elements 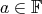 . Elements
of a vector space
. Elements
of a vector space 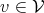 are called vectors.
are called vectors.
While the elements of vector spaces, the vectors, constitute a powerful concept, they are insufficient to describe all the entities required in modelling scientific processes. Additional entities are therefore required. It is not limited to entities introduced later and therefore provided here to clearly distinguish the algebraic structure from the elements.
Definition 17 (Algebra) An algebra 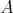 over a field
over a field 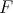 is a vector space equipped with an additional
binary relation (Definition 4)
is a vector space equipped with an additional
binary relation (Definition 4)

A further qualification of the just defined structure may be possible. The availability of the following term allows a more precise classification as found in Definition 56 and in conjunction with Definition 60.
Definition 18 (Graded algebra) In case the algebra admits the decomposition into additive groups of the form


Among the most versatile and useful, almost ubiquitous, algebraic entities are:
Definition 19 (Polynomials) A formal prescription of the form
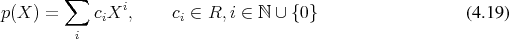
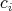 is called a polynomial over the ring (Definition 13)
is called a polynomial over the ring (Definition 13) 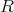 in the variable
in the variable
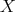 .
.
The variable 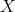 in the purely algebraic definition is a formal symbol and need not be an element of a
field (Definition 14), such as
in the purely algebraic definition is a formal symbol and need not be an element of a
field (Definition 14), such as 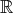 or
or 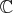 , as in the case of polynomial codes. The algebraic
considerations, however, assert that polynomials defined in this fashion can be added (subtracted) and
multiplied, thus forming a ring (Definition 13). The case that the variables
, as in the case of polynomial codes. The algebraic
considerations, however, assert that polynomials defined in this fashion can be added (subtracted) and
multiplied, thus forming a ring (Definition 13). The case that the variables 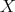 are either from
are either from 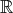 or
or
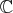 is of particular usefulness in many fields of mathematics, with the field of interpolation
as well integration among them. Then the expression
is of particular usefulness in many fields of mathematics, with the field of interpolation
as well integration among them. Then the expression 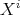 is simply the
is simply the 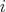 th power of a
variable
th power of a
variable 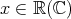 and values can be derived by simple multiplication within their respective
fields.
and values can be derived by simple multiplication within their respective
fields.
 |  |  |