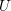 ,
, 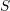 ,
,
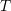 ) refer to tensors and the amount of bars above them identifies the tensor ranking. The
bold lower case letters (
) refer to tensors and the amount of bars above them identifies the tensor ranking. The
bold lower case letters ( ,
,  ) refer to vectors, while the not bold letters are real numbers,
except for
) refer to vectors, while the not bold letters are real numbers,
except for 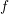 which refer to a real function.
which refer to a real function.
Several operations and identities of first and second order tensors are defined below for fast
consulting. The same notation of the main text is used. The capitalized letters (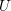 ,
, 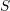 ,
,
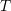 ) refer to tensors and the amount of bars above them identifies the tensor ranking. The
bold lower case letters (
) refer to tensors and the amount of bars above them identifies the tensor ranking. The
bold lower case letters ( ,
,  ) refer to vectors, while the not bold letters are real numbers,
except for
) refer to vectors, while the not bold letters are real numbers,
except for 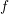 which refer to a real function.
which refer to a real function.
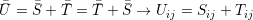 | (A.1) |
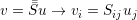 | (A.2) |
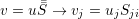 | (A.3) |
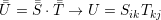 | (A.4) |
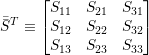 | (A.5) |
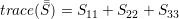 | (A.6) |
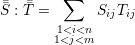 | (A.7) |
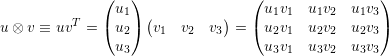 | (A.8) |
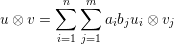 | (A.9) |
In A.9 the vectors 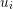 and
and 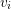 are basis of the space of
are basis of the space of  and
and  respectively.
respectively.
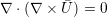 | (A.10) |
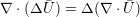 | (A.11) |
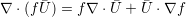 | (A.12) |
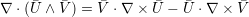 | (A.13) |
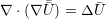 | (A.14) |
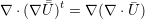 | (A.15) |
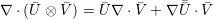 | (A.16) |
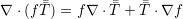 | (A.17) |
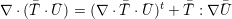 | (A.18) |
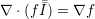 | (A.19) |
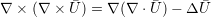 | (A.20) |
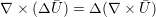 | (A.21) |
 | (A.22) |
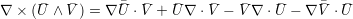 | (A.23) |
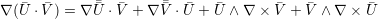 | (A.24) |
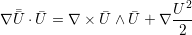 | (A.25) |