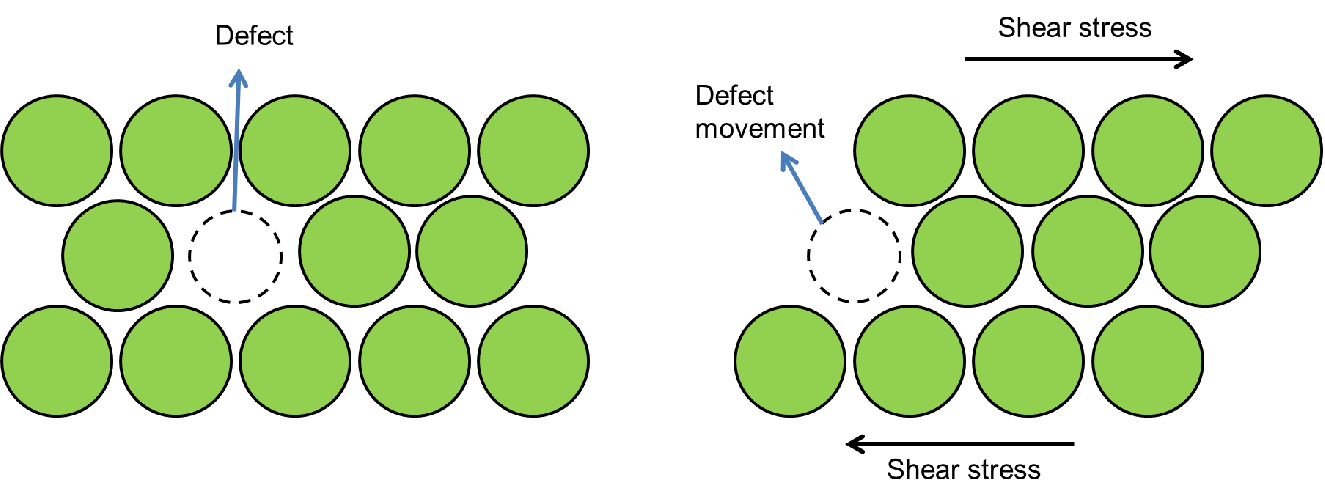
| Figure 2.11.: | Defect movement triggered by shear stress. |
Although hardening modifies the position of the yield point, it is possible to treat both effects separately. The yield point is considered fixed at its first position and the hardening effects are added incrementally whenever needed.
In the literature are a variety of criteria to establish material yielding [39][40][41]. The main challenge is to derive, from the stress tensor, a criterion which triggers yield for different types of materials. For example, in brittle materials it is considered a good criterion that yielding occurs – in fact, brittle materials fracture rather than yield – whenever the largest principal stress surpasses an experimentally established threshold [54]. However, for ductile materials functions of the maximum shear stress is a more suited criterion. Furthermore, anisotropic materials need a different treatment altogether, which considers the directional dependence of the material properties.
Usually, materials used in the semiconductor industry are ductile. For these types of materials there are two most often implemented theories: Tresca theory (or the Maximum Shear Stress) and von Mises theory (or Distortion Energy theory).
The study of yielding was, since the very beginning, motivated by the wish to predict mechanical failure of materials. Yielding is considered as the beginning of a process which will eventually lead to fracture, characterized by the breaking of the bonds between atoms and separation of the material. It is possible to show that the stress required to break the atom bonds is roughly one third of the material’s Young’s modulus [54]. However, ductile materials fail with stress values far smaller than this estimate. For example, aluminium has a theoretical strength of 22GPa, but the stress required for material failure is approximately 100MPa [54]. This inconsistency is justified by the split mechanism of ductile materials. Instead of the rupture of atomic bonds, the material is separated by sliding of atoms as shown in Fig. 2.11.
This phenomenon is related to defects and the way they move inside the materials. Chapter 5 discusses this phenomenon in greater detail. In conclusion, failure in ductile materials is caused by shear deformations. Hence, it is logical to establish a yield criterion in terms of the amount of shear stress a material is able to sustain. This is the principle of the Tresca theory which can be quantified by
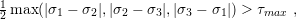 | (2.26) |
where  ,
,  , and
, and  are the principal stresses and
are the principal stresses and  is the maximum shear strain
a material can sustain until it starts to yield (usually obtained experimentally). It is
convenient to to define yield criteria by the principal components, since they are invariant to
any coordinate system.
is the maximum shear strain
a material can sustain until it starts to yield (usually obtained experimentally). It is
convenient to to define yield criteria by the principal components, since they are invariant to
any coordinate system.
Like the Tresca criterion, the von Mises criterion also considers shear deformations as the main mechanism to trigger yielding. However, instead of using the maximum shear stress as the limit of elasticity, the strain energy of shear deformations (distortion energy) is used [55]. In principle there is a critical distortion energy which, if surpassed, pushes the material into the plastic regime. The total strain energy per unit of volume of a body can be calculated in terms of the principal stresses by
where 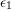 ,
, 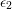 and
and 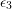 are the principal strains. The relation (2.27) accounts for every
deformation in the body, while for yielding only shear deformations are relevant. Therefore,
the energy stored by normal deformations (hydrostatic energy) must be subtracted from
(2.27) in order to obtain the distortion energy. The hydrostatic energy is given
by
are the principal strains. The relation (2.27) accounts for every
deformation in the body, while for yielding only shear deformations are relevant. Therefore,
the energy stored by normal deformations (hydrostatic energy) must be subtracted from
(2.27) in order to obtain the distortion energy. The hydrostatic energy is given
by
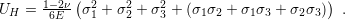 | (2.28) |
Consequently, the distortion energy is given by
Yielding occurs whenever  exceeds a critical energy (
exceeds a critical energy (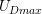 ) [54]. The experimental
determination of
) [54]. The experimental
determination of 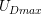 is challenging and it is more convenient to use a critical stress
value. Nonetheless, an uniaxial determination of the critical stress is straightforward to
obtain experimentally and the von Mises criterion remains valid in any situation. Moreover
is challenging and it is more convenient to use a critical stress
value. Nonetheless, an uniaxial determination of the critical stress is straightforward to
obtain experimentally and the von Mises criterion remains valid in any situation. Moreover
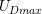 is a material property and must be independent of the load configuration. Hence,
for a body under an uniaxial load the relation (2.29) can be further simplified for
is a material property and must be independent of the load configuration. Hence,
for a body under an uniaxial load the relation (2.29) can be further simplified for
![[(1+ ν)∕6E ]σ2
Max](diss211x.png) , where
, where 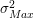 is the critical stress required to yield the material. The
critical stress obtained by the uniaxial stress test can be used in (2.30) to establish a
criterion in terms of stress.
is the critical stress required to yield the material. The
critical stress obtained by the uniaxial stress test can be used in (2.30) to establish a
criterion in terms of stress.
![[ UD] < UDmax
(1+ν)-(σ1 − σ2)2 + (σ1 − σ3 )2 + (σ2 − σ3)2 < (1+ν)σ2Max
6E[ ]1∕2 6E
(σ1 − σ2)2 + (σ1 − σ3)2 + (σ2 − σ3)2 < σMax , (2.30)](diss213x.png)
where the left hand side of the inequality is the equivalent stress which leads to yielding, explicitly described by
![[ ]1∕2
σMises = (σ1 − σ2)2 + (σ1 − σ3)2 + (σ2 − σ3)2 .](diss214x.png) | (2.31) |
The equivalent stress is also known as von Mises stress.
A comparison between the criteria is a good exercise to obtain a better understanding of
both theories. Consider the orthogonal space 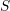 defined by the principal stress vectors. A
point in
defined by the principal stress vectors. A
point in 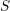 is called stress state. The inequalities (2.26) and (2.30) delineate a region in
is called stress state. The inequalities (2.26) and (2.30) delineate a region in 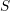 ,
where every stress state internal to the border is in the elastic regime, while the
states at the border and external to it refer to the plastic regime, as shown in
Fig. 2.12.
,
where every stress state internal to the border is in the elastic regime, while the
states at the border and external to it refer to the plastic regime, as shown in
Fig. 2.12.
The Tresca theory is more conservative than the von Mises theory. It predicts a narrower elastic region. The Tresca criterion can be safer from the design point of view, but it could lead the engineer to take unnecessary measures to prevent an unlikely failure. The criterion choice depends on the type of design and personal taste of the designer.
To conclude this session a final remark regarding plasticity in the dimensions of microelectronic devices is warranted. At this scale, the traditional plasticity theory is often unreliable. Sometimes the materials have a different plastic mechanism, while at other times the material is not thick enough for plasticity to take place. Therefore, the classical approach for plasticity is not considered and the plastic models used in the further sections will be presented together with the situation where the mechanism originates.