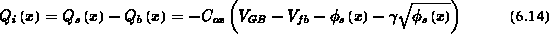
Dieses Modell macht zwei Annahmen über die Ladungsträgerverteilung:
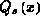ergibt sich
aus der Grundgleichung der MOS-Kapazität 
(
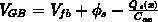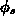ist das Oberflächenpotential
bezogen auf das Bulkpotential).
Damit, mit dem sog. body-Faktor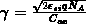 
und der sich aus obigen Annahmen
ergebenden Bulkverarmungsladung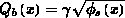 
kann die Inversionsladung angeschrieben werden als:
Der Drainstrom errechnet sich zu [17]:
Der erste Teil, die Driftkomponente, ergibt sich zu:
Der zweite Teil, die Diffusionskomponente, lautet:
Trotz einer Vereinfachung von Gleichung 6.13 für Verarmung und schwache
und starke Inversion (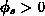
und 
, 
und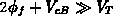 
) können 
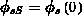und 
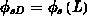aus
nur iterativ errechnet werden. Allerdings fällt gegenüber dem Pao-Sah
Modell die numerische Integration weg. Die Ergebnisse des charge sheet
Modells unterscheiden sich nur um etwa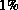 
vom Pao-Sah Modell. Allerdings
sind für komplexe Schaltungssimulationen Modelle wünschenswert, die ohne
iterative Lösung von Gleichungen auskommen.
Fast alle praktisch verwendeten Modelle sind daher geschlossen lösbar.
