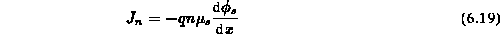
Es gilt also
und aus Abb. 6.2 ergibt sich:
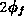ist das klassische Kriterium für starke Inversion, 
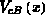wird durch 
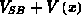ersetzt (
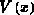ist die auf Source bezogene Kanalspannung). Man kann somit
den Drainstrom anschreiben als:
Es gibt nun mehrere Ansätze,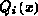 
zu bestimmen:
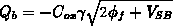konstant über die gesamte Kanallänge und unabhängig
von der Drain-Source-Spannung ist. Damit ist auch 
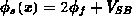konstant entlang des Kanals und Gleichung 6.14
ergibt sich zu:
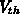ist die Schwellspannung:
Für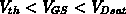 
gilt für den Drainstrom:
Oberhalb der sog. Sättigungsspannung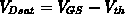 
erhält
man:
Bei der Sättigungsspannung ist am drainseitigen Kanalende die
Inversionsbedingung nicht mehr erfüllt. Bei einem weiteren Erhöhen der
Drainspannung (bei konstanter Gatespannung) wandert dieser sog. pinch-off-Punkt sourcewärts. Zwischen dem Ende des Kanals (pinch-off-Punkt) und Source liegt die Spannung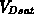 
. Ersetzt man
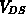durch 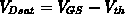, so erhält man aus
Gleichung 6.25 die Gleichung 6.26. Zwischen dem pinch-off-Punkt und dem Drain gibt es keine Inversionsschicht mehr, die
Ladungsträger bewegen sich in dem dort herrschenden starken elektrischen
Feld mit Sättigungsgeschwindigkeit. Mit der Verlagerung des pinch-off-Punkts in Richtung Source sinkt die effektive Kanallänge, der
Drainstrom steigt also mit steigender Drainspannung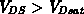 
leicht an. Dies wird in diesem Modell durch den Faktor 
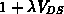(siehe Gleichung 6.26) zu modellieren versucht.
Dieses Modell berücksichtigt die sich entlang des Kanals verändernde
Bulkverarmungsladung. Gleichung 6.27 gilt bis zur
Sättigungsspannung, die sich bei diesem Modell ergibt zu (für 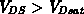ist 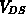durch 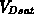zu ersetzen):
wieder zu vereinfachen. Diese Terme kommen vom Ausdruck
in der Gleichung
für 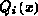. Dieser Term wird nun durch 
approximiert
[42][109]. Die einfachste Methode zur Bestimmung von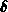 
ist eine Reihenentwicklung des Ausdrucks 
um 
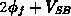nach 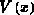. Es
ergibt sich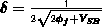 
. In
[6] werden weitere Approximationen für 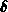zusammengefaßt,
in [24] werden mehrere sekundäre Effekte in 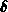subsumiert.
Als Drainstrom ergibt sich für dieses Modell im linearen Bereich (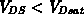
):
Mit einer Sättigungsspannung von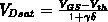 
ergibt sich der Strom im Sättigungsbereich zu:
Die bislang in diesem Abschnitt vorgestellten Formeln gelten nur für den Bereich der starken Inversion. Im folgenden sollen Formeln für geschlossen lösbare MOSFET-Modelle für Gatespannungen unter der Schwellspannung diskutiert werden.
Im Gegensatz zum Gebiet der starken Inversion ist im Gebiet der schwachen
Inversion (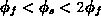
, dies ist gleichbedeutend mit
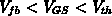) lediglich der Diffusionsterm in der Stromformel
6.3 von Bedeutung. Mit Gleichung 6.5 und der
Einsteinrelation (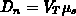
) folgt:
Setzt man Gleichung 6.18 in Gleichung 6.14 ein, so erhält man für die Inversionsladung:
Da mit 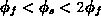der Exponentialterm unter der ersten
Wurzel in Gleichung 6.32 viel kleiner als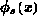 
ist, kann diese erste Wurzel linearisiert werden:
In der schwachen Inversion kann diese Inversionsladung allerdings gegenüber
der Verarmungsladung vernachlässigt werden. Damit müssen die Anteile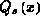 
und 
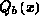aus Gleichung 6.14
näherungsweise gleich sein. Daraus kann man das Oberflächenpotential für
schwache Inversion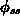 
bestimmen [65]:
Damit kann der Drainstrom in der schwachen Inversion ausgedrückt werden als:
Man kann diese Formel umschreiben als [6]:
Der Drainstrom unterhalb der Schwellspannung steigt somit exponentiell mit der Gatespannung. Da die Kurven für starke und schwache Inversion bei den geschlossen lösbaren MOSFET-Modellen nicht stetig ineinander übergehen, soll im nächsten Abschnitt ein geschlossen lösbares Modell vorgestellt werden, das diesen Nachteil nicht aufweist. Außerdem soll noch erwähnt werden, daß natürlich in der Praxis keine konstante Beweglichkeit in den Schaltungsmodellen verwendet wird, sondern eine effektive, in Abhängigkeit von diversen Größen (etwa Spannungen) modellierte Beweglichkeit nach der Herleitung der Gleichungen in diese eingesetzt wird.
