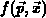Bei der Berechnung der Implantationsprofile mittels der
Boltzmanngleichung - Beschreibungen sind etwa in [Chr80],
[Tak83], [Gil85a], [Tak85], [Gil86] oder
[Tak86] zu finden - wird die Veränderung der Impulsverteilung
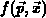während des Eindringens des Ionenstrahls in das
Target betrachtet. Mit
lautet die Boltzmann-Transportgleichung für den dreidimensionalen
Fall für den Punkt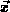 
wobei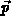 
der Impuls, 
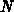die atomare Dichte des Targets, 
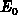die Anfangsenergie und 
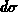die Wahrscheinlichkeit einer
Kollision des Ions mit einem Targetatom ist.
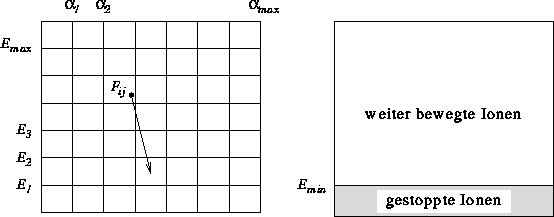
Abbildung: Boltzmannverteilung:
Kollisionsvorgang in der Verteilungsmatrix (nach Giles [Gil86]).
Ionen können nun vom Zustand (Impuls) 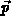durch einen
Kollisionsvorgang in den Zustand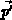 
übergehen und umgekehrt.
Zu Beginn bewegen sich alle Ionen mit gleicher Geschwindigkeit
(definiert durch die Anfangsenergie 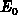) in die gleiche Richtung
(gegeben durch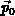 
), das heißt, daß die Impulsverteilung an
der Oberfläche eine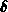 
-Funktion ist. Nach jedem Schritt wird
jener Anteil der Verteilungsfunktion, dessen Energie unter einen
gewissen Schwellwert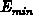 
fällt, am Ort 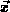abgespeichert.
Außerdem muß dieser Betrag aus der Verteilungsfunktion des
Ionenstrahles entfernt werden. Der Rest wird weiterverfolgt bis auch
diese Ionen ihre Energie soweit verloren haben, daß sie zum
Stillstand kommen.
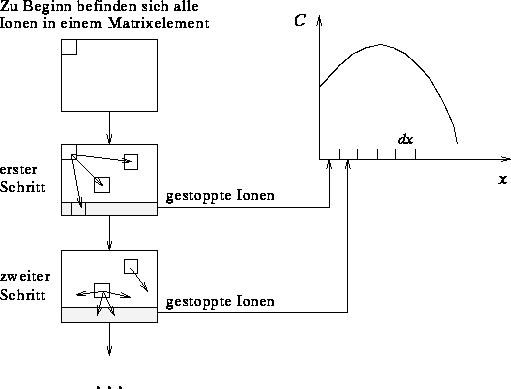
Abbildung: Lösung der Boltzmann-Transportgleichung für die Bestimmung von
Implantationsprofilen (nach Giles [Gil86]).
Für eindimensionale Rechnungen kann 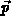durch die Energie 
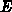und den Neigungswinkel 
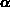der Bewegungsrichtung zur
Koordinatenachse ersetzt werden. Für die numerische Berechnung wird
die Verteilungsfunktion im eindimensionalen Fall nach
Giles [Gil86] als zweidimensionale Matrix mit den Einträgen
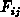für Teilchen, die sich mit der Energie 
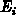in Richtung
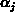bewegen (siehe Abb. 1.1), repräsentiert.
Die Ermittlung des ortsabhängigen Implantationsprofiles nach dieser
Methode kann der Abb. 1.2 entnommen werden.
Im zweidimensionalen Fall müssen noch der azimutale Winkel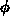 
und
die zweite Ortskoordinate 
hinzugenommen werden. Es muß dann der
vierdimensionale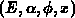 
-Raum diskretisiert werden, und
man benötigt eine vierdimensionale Matrix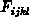 
mit
Übergansfunktionen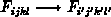 
[Gil86]. Eine exakte Simulation wird hier aber
durch den begrenzten Speicherplatz und die hohen Rechenzeiten
unmöglich.
Im dreidimensionalen Fall muß schließlich ein fünfdimensionaler
Raum (die zweite laterale Koordinate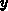 
wird noch zusätzlich
berücksichtigt) diskretisiert werden. Das ergibt noch einmal eine
erhebliche Steigerung sowohl im Speicheraufwand als auch im
Rechenzeitbedarf. Daher sind dreidimensionale Simulationen basierend
auf der Boltzmann-Transport Gleichung nicht konkurenzfähig zu
Monte-Carlo Methoden und es sind auch derzeit keine dreidimensionalen
Anwendungen bekannt.
Bei nicht zu hohen Genauigkeitsanforderungen im zweidimensionalen Raum oder für eindimensionale Berechnungen ist diese Methode aber der noch später skizzierten Monte-Carlo Methode von der Rechenzeit her überlegen. Die Lösung der Boltzmanngleichung liefert im allgemeinen glattere Dotierungsprofile als die Monte-Carlo Methode. Mit beiden Techniken können Effekte wie Damage (Zerstörung der Kristallstruktur), Rückstreuung der Ionen oder Recoils (aus dem Kristall ausgeschlagene Atome) mitgerechnet werden.
