


Next: 2.2 MOS-Transistor
Up: 2. Schrödinger-Poisson-Solver
Previous: 2. Schrödinger-Poisson-Solver
Unterabschnitte
Für die hier vorgesehene Untersuchung empfiehlt es sich von dem in
Abschnitt 1.4.3 vorgestellten einfachen Modell einer
Einteilchen-Schrödinger-Gleichung mit einer effektiven Masse und einer
nichtparabolischen Dispersionsrelation (1.15)
auszugehen. Ausgangspunkt ist die zeitunabhängige
Schrödinger-Gleichung (1.3) für ein einzelnes Teilchen in der eine gegeben
Potenzialverteilung eingesetzt wird.
Unter Verwendung einer skalaren effektiven Masse 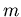 lässt sich der
Operator des Bandformfaktors mit dem Tensor der inversen Masse
lässt sich der
Operator des Bandformfaktors mit dem Tensor der inversen Masse
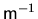 wie folgt darstellen:
wie folgt darstellen:
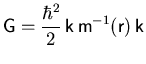 |
(2.1) |
Der Operator
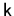 des Wellenvektors
des Wellenvektors
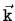 lautet dabei in der
Ortsdarstellung
lautet dabei in der
Ortsdarstellung
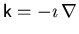 . Es ist zu beachten,
dass die Operatoren
. Es ist zu beachten,
dass die Operatoren
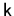 und
und
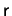 nicht vertauschbar sind.
Durch die symmetrische Schreibweise in
(2.1) ist der Operator
nicht vertauschbar sind.
Durch die symmetrische Schreibweise in
(2.1) ist der Operator
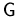 jedoch selbstadjungiert. Die Verwendung des Begriffs einer effektiven
Masse war notwendig, um das Vielteilchenproblem auf ein äquivalentes
Einteilchenproblem zu reduzieren. In der Praxis wird also durch
Einführen einer parabolischen Dispersionsrelation zwischen Energie und
Wellenvektor, in der die effektive Masse als Parameter eingeht, der
Einfluss des Kristallgitters in einer einfachen Einteilchen-Gleichung
zum Ausdruck gebracht. Diese Vereinfachung ist jedoch nicht
ausreichend wenn Ladungsträger mit höheren Energien untersucht werden
sollen. Die Dispersionsrelation kann wie in Abschnitt
1.4.3 beschrieben nach dem Ansatz von Kane um einen
zusätzlichen Nichtparabolizitätskoeffizienten
jedoch selbstadjungiert. Die Verwendung des Begriffs einer effektiven
Masse war notwendig, um das Vielteilchenproblem auf ein äquivalentes
Einteilchenproblem zu reduzieren. In der Praxis wird also durch
Einführen einer parabolischen Dispersionsrelation zwischen Energie und
Wellenvektor, in der die effektive Masse als Parameter eingeht, der
Einfluss des Kristallgitters in einer einfachen Einteilchen-Gleichung
zum Ausdruck gebracht. Diese Vereinfachung ist jedoch nicht
ausreichend wenn Ladungsträger mit höheren Energien untersucht werden
sollen. Die Dispersionsrelation kann wie in Abschnitt
1.4.3 beschrieben nach dem Ansatz von Kane um einen
zusätzlichen Nichtparabolizitätskoeffizienten
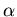 ergänzt werden, und lautet
für eine isotrope effektive Masse
ergänzt werden, und lautet
für eine isotrope effektive Masse 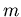 wie folgt.
wie folgt.
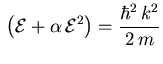 |
(2.2) |
Wir wollen diese Korrektur nun auch bei der
Betrachtung eines quantisierten Systems einbeziehen und fordern daher,
dass der Operator der kinetischen Energie folgende Relation erfüllen muss:
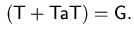 |
(2.3) |
(2.3)
entspricht (2.2) in Operatorschreibweise.
Für Silizium liegt der Wert des Koeffizienten
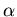 bei
0.5
bei
0.5 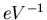 .
.
Abbildung 2.1:
Analytische Dispersionsrelationen zu verschiedenen
Werten des Nichtparabolizitätskoeffizienten.
|
|
Abbildung 2.1 soll die resultierende
Dispersionsrelation (2.2) für einige Werte
von
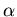 veranschaulichen. Für den Wert Null erhält man wieder
den parabolischen Fall aus Gleichung
(2.1). Für Teilchen mit einer Energie
über 300
veranschaulichen. Für den Wert Null erhält man wieder
den parabolischen Fall aus Gleichung
(2.1). Für Teilchen mit einer Energie
über 300 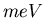 erkennt man bereits einen sichtbaren Unterschied
in der parabolischen und der nichtparabolischen Dispersionsrelation.
erkennt man bereits einen sichtbaren Unterschied
in der parabolischen und der nichtparabolischen Dispersionsrelation.
Ausgehend vom Ansatz mit Bloch-Funktionen
nach (1.8), wird ein Separationsansatz gewählt bei
dem die Elektronen in der Ebene parallel zur Quantisierungsrichtung
als freie Teilchen betrachtet werden. An Stelle einer
dreidimensionalen ebenen Welle verwenden wir nun eine ebene Welle in
der Normalebene zur Quantisierungsrichtung und eine einhüllende
Funktion
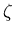 in der Quantisierungsrichtung.
in der Quantisierungsrichtung.
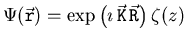 |
(2.4) |
Diesen Separationsansatz setzen wir nun in die Schrödinger-Gleichung ein.
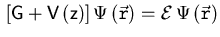 |
(2.5) |
Für den Hamilton-Operator wurden hier nur jene Terme verwendet, die
das Elektronensystem beschreiben. Der Operator
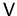 beschreibt die
Wirkung des für die Quantisierung verantwortlichen Potenzials und soll
nur von der Quantisierungsrichtung
beschreibt die
Wirkung des für die Quantisierung verantwortlichen Potenzials und soll
nur von der Quantisierungsrichtung 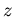 abhängen. Aus der gewählten
Definition nach (2.3) ergibt sich der
Operator der kinetischen Energie
abhängen. Aus der gewählten
Definition nach (2.3) ergibt sich der
Operator der kinetischen Energie
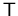 als Operatorfunktion von
als Operatorfunktion von
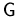 . Bei (2.5)
beschränken wir uns auf den parabolischen Fall
. Bei (2.5)
beschränken wir uns auf den parabolischen Fall
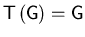 . Wir nehmen hier weiters an, dass der
Tensor der inversen effektiven Masse diagonal ist.
. Wir nehmen hier weiters an, dass der
Tensor der inversen effektiven Masse diagonal ist.
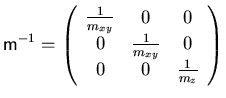 |
(2.6) |
Die in (2.6) vorkommenden Massen
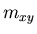 und
und
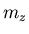 sind dabei skalare Konstanten.
Den Operator des Wellenvektors spalten wir dementsprechend in zwei
Komponenten für die Quantisierungsrichtung und die Parallelebene auf.
sind dabei skalare Konstanten.
Den Operator des Wellenvektors spalten wir dementsprechend in zwei
Komponenten für die Quantisierungsrichtung und die Parallelebene auf.
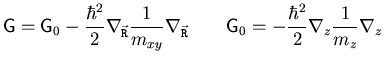 |
(2.7) |
Wir wenden nun den Operator
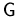 auf die im
Separationsansatz (2.4) verwendete
Wellenfunktion an. Der in (2.7) vorkommende
Operator
auf die im
Separationsansatz (2.4) verwendete
Wellenfunktion an. Der in (2.7) vorkommende
Operator
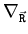 wirkt nur auf die ebene Welle in
Parallelrichtung.
Der Operator
wirkt nur auf die ebene Welle in
Parallelrichtung.
Der Operator
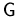 kann also für den verwendeten
Separationsansatz als
kann also für den verwendeten
Separationsansatz als
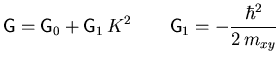 |
(2.8) |
angeschrieben werden. Die hier verwendete Nomenklatur mit
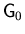 und
und
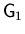 soll der später verwendeten Reihenentwicklung nach dem
Parallel-Wellenvektor dienen.
soll der später verwendeten Reihenentwicklung nach dem
Parallel-Wellenvektor dienen.
Setzen wir nun die Wellenfunktion (2.4) in die
Schrödinger-Gleichung (2.5) mit dem
Operator
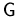 aus (2.8) ein und
verwenden die Separationsvariable
aus (2.8) ein und
verwenden die Separationsvariable
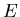 . Der Separationsansatz
liefert in der Parallelebene einen quadratischen Zusammenhang zwischen
der Separationsvariable
. Der Separationsansatz
liefert in der Parallelebene einen quadratischen Zusammenhang zwischen
der Separationsvariable
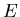 und der Energie
und der Energie
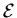 .
.
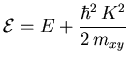 |
(2.9) |
In der Quantisierungsrichtung ergeben sich aus der eindimensionalen
Schrödinger-Gleichung
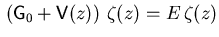 |
(2.10) |
diskrete Eigenwerte
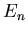 für die Separationsvariable
für die Separationsvariable
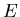 .
.
Abbildung 2.2:
Skizze zum Begriff der Subbänder.
|
|
Die Skizze 2.2 veranschaulicht den
Zusammenhang (2.9). Ein Elektron mit dem diskreten
Eigenwert
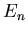 und der entsprechenden Eigenfunktion
und der entsprechenden Eigenfunktion
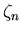 befindet sich dann im Subband
befindet sich dann im Subband 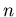 .
.
Im parabolischen Fall ergab der
Separationsansatz (2.4) für die einhüllende
Funktion
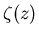 die eindimensionale
Schrödinger-Gleichung (2.10). Für die Lösung dieses
Eigenwertproblems im feldfreien Fall
die eindimensionale
Schrödinger-Gleichung (2.10). Für die Lösung dieses
Eigenwertproblems im feldfreien Fall
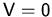 mit geeigneten, einfachen Randbedingungen verwenden
wir die Darstellung des Operators
mit geeigneten, einfachen Randbedingungen verwenden
wir die Darstellung des Operators
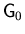 im Ortsraum und
bezeichnen die Lösungen mit
im Ortsraum und
bezeichnen die Lösungen mit 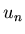 .
.
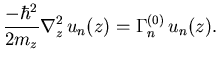 |
(2.11) |
Der Einfachheit halber setzen wir den Koordinatenursprung an die
Grenzfläche zwischen Oxid und Halbleiter. An dieser Stelle haben wir
eine Diskontinuität in der Leitungsbandkante von etwa
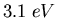 für den Fall eines MOS-Transistors mit Siliziumsubstrat. Dies nehmen
wir zum Anlass die Randbedingungen wie folgt zu definieren. Die
Wellenfunktionen sollen am Koordinatenursprung und im Unendlichen
verschwinden. Wir beschränken unsere Untersuchung also auf den Fall
einer vernachlässigbaren Penetration der Wellenfunktionen in das
Oxid. Für die praktische Umsetzung wird natürlich auch die zweite
Randbedingung nicht im Unendlichen sondern bei einer sinnvoll
gewählten Entfernung
für den Fall eines MOS-Transistors mit Siliziumsubstrat. Dies nehmen
wir zum Anlass die Randbedingungen wie folgt zu definieren. Die
Wellenfunktionen sollen am Koordinatenursprung und im Unendlichen
verschwinden. Wir beschränken unsere Untersuchung also auf den Fall
einer vernachlässigbaren Penetration der Wellenfunktionen in das
Oxid. Für die praktische Umsetzung wird natürlich auch die zweite
Randbedingung nicht im Unendlichen sondern bei einer sinnvoll
gewählten Entfernung
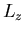 vom Oxid angesetzt. Weiters sollen die
Eigenfunktionen auf Eins normiert sein. Mit den genannten Bedingungen
ergeben sich die Lösungen zu (2.11) als
vom Oxid angesetzt. Weiters sollen die
Eigenfunktionen auf Eins normiert sein. Mit den genannten Bedingungen
ergeben sich die Lösungen zu (2.11) als
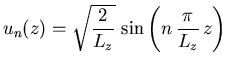 |
(2.12) |
und die korrespondierenden Eigenwerte als
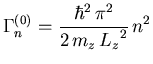 |
(2.13) |
Die Funktionen (2.12) werden als Basis für die
Berechnungen im Simulator benutzt.
Um die Nichtparabolizität in der Dispersionsrelation der Energie
nach (2.3) zu berücksichtigen, führen wir
die Operatoren
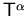 und
und
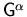 ein.
ein.
Ziel ist es, eine Darstellung des Operators der kinetischen Energie
zu finden, die in einem Simulator umsetzbar ist. Der Vorteil der
neuen Operatoren liegt in der deutlich einfacheren Form der
Gleichung (2.3), in der der
Nichtparabolizitätskoeffizient nicht mehr explizit aufscheint.
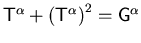 |
(2.15) |
Mit dieser Darstellung ist das Problem, dass die Operatoren
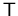 und
und
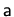 in (2.3) nicht
vertauschbar sind, gelöst. (2.15)
definiert einen einfachen Zusammenhang zwischen den Eigenfunktionen
und Eigenwerten der beiden Operatoren
in (2.3) nicht
vertauschbar sind, gelöst. (2.15)
definiert einen einfachen Zusammenhang zwischen den Eigenfunktionen
und Eigenwerten der beiden Operatoren
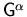 und
und
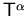 . Es gilt folgender
Zusammenhang ([10, 2.3]): Ein Operator sei aus der Anwendung
einer Operatorfunktion
. Es gilt folgender
Zusammenhang ([10, 2.3]): Ein Operator sei aus der Anwendung
einer Operatorfunktion
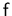 aus dem Operator
aus dem Operator
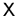 hervorgegangen, wobei sich die Operatorfunktion durch eine Potenzreihe
in
hervorgegangen, wobei sich die Operatorfunktion durch eine Potenzreihe
in
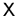 darstellen lässt. Dieser neue Operator hat dann die
gleichen Eigenfunktionen wie der Ausgangsoperator und seine Eigenwerte
ergeben sich aus der Anwendung der skalarwertigen Funktion
darstellen lässt. Dieser neue Operator hat dann die
gleichen Eigenfunktionen wie der Ausgangsoperator und seine Eigenwerte
ergeben sich aus der Anwendung der skalarwertigen Funktion 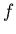 auf die
Eigenwerte des Operators
auf die
Eigenwerte des Operators
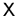 . Dies lässt sich auf den Operator
. Dies lässt sich auf den Operator
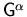 mit der Funktion
mit der Funktion
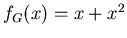 anwenden.
Andererseits gilt dies auch für die Umkehrfunktion.
anwenden.
Andererseits gilt dies auch für die Umkehrfunktion.
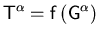 |
(2.16) |
Die Eigenfunktionen beider Operatoren sind ident. Aus den
Eigenwerten
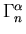 des Operators
des Operators
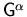 lassen
sich die Eigenwerte des Operators
lassen
sich die Eigenwerte des Operators
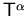 als
als
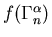 angeben. Dazu benötigt man die Umkehrfunktion.
angeben. Dazu benötigt man die Umkehrfunktion.
Da es sich um Energieeigenwerte handelt, wird nur die positive Lösung
der quadratischen Gleichung berücksichtigt.
Tabelle 2.1:
Zusammenfassung der Eigenwerte und Eigenfunktionen der
voneinander abhängigen Operatoren.
| Operator |
Eigenfunktion |
Eigenwert |
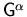 |
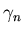 |
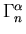 |
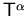 |
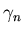 |
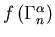 |
|
Die Zusammenhänge zwischen den Eigenwerten und Eigenfunktionen der
Operatoren
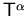 und
und
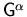 sind in der Tabelle 2.1 zusammengefasst.
Durch die Umformung (2.14) ist es also gelungen,
die Eigenwerte des Operators der kinetischen Energie als Funktion der
Eigenwerte des Operators
sind in der Tabelle 2.1 zusammengefasst.
Durch die Umformung (2.14) ist es also gelungen,
die Eigenwerte des Operators der kinetischen Energie als Funktion der
Eigenwerte des Operators
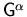 anzuschreiben. Die
Umformung muss dabei in der Basis bestehend aus den Eigenfunktionen
des Operators
anzuschreiben. Die
Umformung muss dabei in der Basis bestehend aus den Eigenfunktionen
des Operators
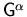 erfolgen. Dazu führen wir den
Projektionsoperator auf die Eigenfunktionen des
Operators
erfolgen. Dazu führen wir den
Projektionsoperator auf die Eigenfunktionen des
Operators
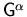
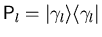 |
(2.18) |
ein und erhalten aus der Vollständigkeitsrelation
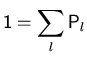 |
(2.19) |
folgende Entwicklung des Operators der kinetischen Energie.
Die Summation über 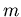 wurde in (2.20)
weggelassen, da die gemischten Matrixelemente
wurde in (2.20)
weggelassen, da die gemischten Matrixelemente
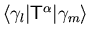 für
für 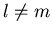 verschwinden. Mit (2.20) ergibt sich folgende
formale Definition des Operators der kinetischen Energie.
verschwinden. Mit (2.20) ergibt sich folgende
formale Definition des Operators der kinetischen Energie.
Der Zusammenhang (2.21) ergibt also eine Darstellung
des Operators der kinetischen Energie mit den Eigenfunktionen und Eigenenergien des Operators
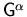 .
.
Der Operator der kinetischen Energie ist
nach (2.21) als Funktion des Operators
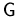 definiert. Mit dem Separationsansatz (2.4)
und einer parabolischen Dispersionsrelation ergab sich
nach (2.8) ein vom Parallel-Wellenvektor
abhängiger Operator
definiert. Mit dem Separationsansatz (2.4)
und einer parabolischen Dispersionsrelation ergab sich
nach (2.8) ein vom Parallel-Wellenvektor
abhängiger Operator
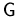 . Die Veränderung, die sich durch die
nichtparabolische Dispersionsrelation (2.2)
ergibt, soll nun mittels der Störungsrechnung behandelt werden. Wie
wir im folgenden zeigen, lässt sich so in konsistenter Weise eine
nichtparabolische Dispersionsrelation für die einzelnen Subbänder
ableiten.
. Die Veränderung, die sich durch die
nichtparabolische Dispersionsrelation (2.2)
ergibt, soll nun mittels der Störungsrechnung behandelt werden. Wie
wir im folgenden zeigen, lässt sich so in konsistenter Weise eine
nichtparabolische Dispersionsrelation für die einzelnen Subbänder
ableiten.
Als erster Schritt wird angenommen, dass sich der Operator der kinetischen
Energie in eine Taylor-Reihe nach dem Parallel-Wellenvektor entwickeln
lässt. Im Rahmen der nichtparabolischen
Dispersionsrelation (2.2) kann diese Reihe
beim Glied der Ordnung vier abgebrochen werden.
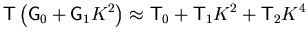 |
(2.22) |
Die Eigenwerte
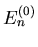 und Eigenfunktionen
und Eigenfunktionen
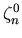 sind die Lösungen des ungestörten Problems.
sind die Lösungen des ungestörten Problems.
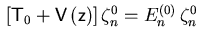 |
(2.23) |
Für die Störung
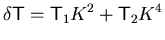 |
(2.24) |
ergibt sich dann aus der Störungsrechnung erster Ordnung (siehe
Anhang A.1) folgende Korrektur für die Eigenwerte.
Die Matrixelemente
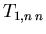 und
und
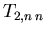 des
Operators
des
Operators
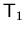 beziehungsweise
beziehungsweise
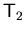 sind dabei wie folgt
definiert.
sind dabei wie folgt
definiert.
Um eine Entwicklung bis zu Termen vierter
Ordnung zu erhalten, verwenden wir zusätzlich die Korrekturen
aus der Störungsrechnung zweiter Ordnung. Diese führen auf Terme in
denen die Parallelkomponente des Wellenvektors mit der Ordnung vier
vorkommt.
Insgesamt folgt aus der Störungsrechnung folgende Abhängigkeit des
Energieeigenwerts vom Wellenvektor.
Einen solchen Ansatz verfolgen auch zum Beispiel die Autoren in
[11]. Zur Charakterisierung der einzelnen Subbänder ist die
Einführung einer zum nicht quantisierten Fall analogen
Dispersionsrelation für jedes Subband mit den Parametern effektive
Masse
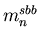 und Nichtparabolizitätskoeffizient
und Nichtparabolizitätskoeffizient
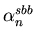 zielführend.
zielführend.
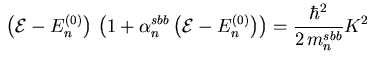 |
(2.29) |
Um die hier eingeführten Subbandparameter zu erhalten, lösen wir die
quadratische Gleichung (2.29) nach den Eigenwerten
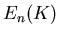 , berücksichtigen dabei nur Terme bis vierter
Ordnung in
, berücksichtigen dabei nur Terme bis vierter
Ordnung in  , und führen einen Koeffizientenvergleich mit
Gleichung (2.28) durch.
Die dabei auftretende Wurzelfunktion kann,
im Rahmen einer Beschränkung auf Terme bis vierter Ordnung, für den
Betrag der Parallelkomponente des Wellenvektors, durch die Entwicklung
, und führen einen Koeffizientenvergleich mit
Gleichung (2.28) durch.
Die dabei auftretende Wurzelfunktion kann,
im Rahmen einer Beschränkung auf Terme bis vierter Ordnung, für den
Betrag der Parallelkomponente des Wellenvektors, durch die Entwicklung
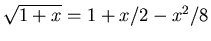 ersetzt werden. Für den
Koeffizientenvergleich verwenden wir somit
statt (2.29) folgende Näherung.
ersetzt werden. Für den
Koeffizientenvergleich verwenden wir somit
statt (2.29) folgende Näherung.
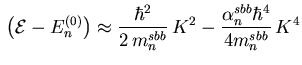 |
(2.30) |
Aus dem Koeffizientenvergleich erhalten wir folgende Subbandparameter.
Die Matrixelemente in (2.31) müssen in
der Basis der Eigenfunktionen des Operators
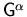 und mit den Eigenwerten der
Gleichung (2.23) berechnet werden.
und mit den Eigenwerten der
Gleichung (2.23) berechnet werden.



Next: 2.2 MOS-Transistor
Up: 2. Schrödinger-Poisson-Solver
Previous: 2. Schrödinger-Poisson-Solver
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
![\includegraphics[]{Schroedinger/Evonk-graph-fin.eps}](img152.png)
![]() aus (2.8) ein und
verwenden die Separationsvariable
aus (2.8) ein und
verwenden die Separationsvariable
![]() . Der Separationsansatz
liefert in der Parallelebene einen quadratischen Zusammenhang zwischen
der Separationsvariable
. Der Separationsansatz
liefert in der Parallelebene einen quadratischen Zusammenhang zwischen
der Separationsvariable
![]() und der Energie
und der Energie
![]() .
.
![]() des Operators
des Operators
![]() lassen
sich die Eigenwerte des Operators
lassen
sich die Eigenwerte des Operators
![]() als
als
![]() angeben. Dazu benötigt man die Umkehrfunktion.
angeben. Dazu benötigt man die Umkehrfunktion.
![]() und
und
![]() sind in der Tabelle 2.1 zusammengefasst.
Durch die Umformung (2.14) ist es also gelungen,
die Eigenwerte des Operators der kinetischen Energie als Funktion der
Eigenwerte des Operators
sind in der Tabelle 2.1 zusammengefasst.
Durch die Umformung (2.14) ist es also gelungen,
die Eigenwerte des Operators der kinetischen Energie als Funktion der
Eigenwerte des Operators
![]() anzuschreiben. Die
Umformung muss dabei in der Basis bestehend aus den Eigenfunktionen
des Operators
anzuschreiben. Die
Umformung muss dabei in der Basis bestehend aus den Eigenfunktionen
des Operators
![]() erfolgen. Dazu führen wir den
Projektionsoperator auf die Eigenfunktionen des
Operators
erfolgen. Dazu führen wir den
Projektionsoperator auf die Eigenfunktionen des
Operators
![]()
![]() definiert. Mit dem Separationsansatz (2.4)
und einer parabolischen Dispersionsrelation ergab sich
nach (2.8) ein vom Parallel-Wellenvektor
abhängiger Operator
definiert. Mit dem Separationsansatz (2.4)
und einer parabolischen Dispersionsrelation ergab sich
nach (2.8) ein vom Parallel-Wellenvektor
abhängiger Operator
![]() . Die Veränderung, die sich durch die
nichtparabolische Dispersionsrelation (2.2)
ergibt, soll nun mittels der Störungsrechnung behandelt werden. Wie
wir im folgenden zeigen, lässt sich so in konsistenter Weise eine
nichtparabolische Dispersionsrelation für die einzelnen Subbänder
ableiten.
. Die Veränderung, die sich durch die
nichtparabolische Dispersionsrelation (2.2)
ergibt, soll nun mittels der Störungsrechnung behandelt werden. Wie
wir im folgenden zeigen, lässt sich so in konsistenter Weise eine
nichtparabolische Dispersionsrelation für die einzelnen Subbänder
ableiten.
![]() und Eigenfunktionen
und Eigenfunktionen
![]() sind die Lösungen des ungestörten Problems.
sind die Lösungen des ungestörten Problems.