


Next: 2.4 Poisson-Gleichung
Up: 2. Schrödinger-Poisson-Solver
Previous: 2.2 MOS-Transistor
Unterabschnitte
Bei Heterostrukturen handelt es sich um Halbleiterbauelemente die aus
mehreren Schichten von Halbleiterlegierungen bestehen ([29]).
Mittels Molekularstrahl-Epitaxie oder dem Aufwachsen aus der
gasförmigen Phase können heute sehr dünne Schichten mit einem abrupten
Übergang aufeinander aufgebracht werden. Die Veränderung der Legierung
ermöglicht eine gezielte Beeinflussung des Bandabstands der
Halbleitermaterialien dieser einzelnen Schichten. Dieser Effekt führt
zur Ausbildung eines Kanals wenn eine Schicht mit einem geringeren
Bandabstand zwischen zwei Schichten mit einem großen Bandabstand
eingeschlossen wird. Die verwendeten Materialen weisen sehr hohe
Elektronenbeweglichkeiten auf, und eignen sich daher sehr gut für
Hochfrequenzanwendungen. Der Heterostruktur-Feldeffekttransistor
(HFET) ist ein sehr erfolgreiches Bauelement, das auf diesem Effekt
aufbaut.
Durch die Möglichkeit sehr dünne Schichten mit abrupten Übergängen zu
erzeugen ist bei Heterostrukturen die Untersuchung von Quanteneffekte
eine wichtige Aufgabe.
Die Schrödinger-Gleichung
wird nun
in einem Gebiet gelöst, dass sich über mehrere Schichten mit
unterschiedlichen Materialparametern erstreckt. In der
Quantisierungsrichtung sind die Elektronenmassen
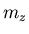 ,
,
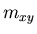 und
der Nichtparabolizitätskoeffizient
und
der Nichtparabolizitätskoeffizient
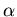 somit von der z-Koordinate abhängig.
Die im folgenden beschriebene numerische Methode ermöglicht die Lösung
der Schrödinger-Gleichung für eine Heterostruktur unter
Berücksichtigung der nichtparabolischen
Dispersionrelation (2.2).
somit von der z-Koordinate abhängig.
Die im folgenden beschriebene numerische Methode ermöglicht die Lösung
der Schrödinger-Gleichung für eine Heterostruktur unter
Berücksichtigung der nichtparabolischen
Dispersionrelation (2.2).
Der Operator der kinetischen Energie
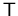 soll wieder
durch (2.3) definiert sein. Um in der
Basis (2.12) eine eindimensionale
Schrödinger-Gleichung anschreiben zu können, greifen wir auf die
Störungsrechnung zurück.
soll wieder
durch (2.3) definiert sein. Um in der
Basis (2.12) eine eindimensionale
Schrödinger-Gleichung anschreiben zu können, greifen wir auf die
Störungsrechnung zurück.
Für die ortsabhängigen Materialparametern betrachten wir die
folgenden Operatoren.
Es gelten für die Operatoren aus (2.54)
und (2.7) die in
Tabelle 2.4 angegebenen Eigenfunktionen und
Eigenwerte.
Tabelle 2.4:
Zusammenhang der Eigenwerte und Eigenfunktionen der
voneinander abhängigen Operatoren bei Heterostrukturen.
| Operator |
Eigenfunktion |
Eigenwert |
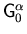 |
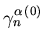 |
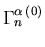 |
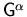 |
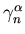 |
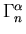 |
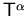 |
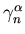 |
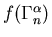 |
|
Wir wenden nun den Separationsansatzes (2.4)
auf den Operator
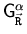 an.
an.
Es ergibt sich also ein vom Wellenvektor abhängiger Operator
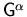 .
.
Der Term
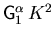 wird nun als Störung
zum ungestörten Eigenwertproblem für
wird nun als Störung
zum ungestörten Eigenwertproblem für
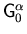 betrachtet.
Die Eigenwerte und Eigenfunktionen des Operators
betrachtet.
Die Eigenwerte und Eigenfunktionen des Operators
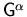 lassen sich somit über die Störungsrechnung aus den Eigenfunktionen und
Eigenwerten des Operators
lassen sich somit über die Störungsrechnung aus den Eigenfunktionen und
Eigenwerten des Operators
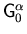 berechnen. Der
Term
berechnen. Der
Term 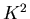 kann dabei jeweils aus den benötigten Matrixelementen
herausgezogen werden. Aus der Störungsrechnung erster Ordnung folgt zum Beispiel:
kann dabei jeweils aus den benötigten Matrixelementen
herausgezogen werden. Aus der Störungsrechnung erster Ordnung folgt zum Beispiel:
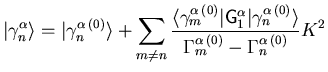 |
|
|
(2.57) |
Als Näherung gilt somit folgende Darstellung
für die Eigenwerte und Eigenfunktionen des Operators
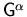 .
.
Aus (2.15) ergibt sich wieder
die Spektraldarstellung des Operators der kinetischen Energie.
Der Eigenwert
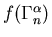 wird dabei
gemäß der Näherung (2.60) in eine
Potenzreihe der Ordnung vier in
wird dabei
gemäß der Näherung (2.60) in eine
Potenzreihe der Ordnung vier in 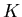 entwickelt.
entwickelt.
Der Projektionsoperator wird mit der Darstellung der Eigenfunktionen
des Operators
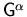 aus (2.60)
näherungsweise wie folgt angeschrieben.
aus (2.60)
näherungsweise wie folgt angeschrieben.
Wir setzen nun die beiden Approximationen (2.63)
und (2.62) in (2.61) ein und
berücksichtigen nur Terme in 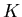 bis zur Ordnung 2.
bis zur Ordnung 2.
![$\displaystyle {}
{\ensuremath{{\ensuremath{\mathsf{T}}}}}^{{\ensuremath{\alpha}...
...nsuremath{\mathsf{P}}}_n^{{\ensuremath{\alpha}}}(0,0)
\right]
{K}^2
\right\}$](img339.png) |
|
|
(2.62) |
Aus einem Koeffizientenvergleich der Gleichungen (2.64)
und (2.22) erhalten wir dann folgende Operatoren
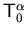 und
und
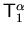 .
.
Diese Operatoren kann man nun verwenden um
nach (2.31) die Subbandmassen
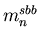 zu berechnen und die eindimensionale Schrödinger-Gleichung
in Matrixform in der Basis der Eigenfunktionen
zu berechnen und die eindimensionale Schrödinger-Gleichung
in Matrixform in der Basis der Eigenfunktionen 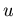 anzuschreiben.
anzuschreiben.



Next: 2.4 Poisson-Gleichung
Up: 2. Schrödinger-Poisson-Solver
Previous: 2.2 MOS-Transistor
C. Troger: Modellierung von Quantisierungseffekten in Feldeffekttransistoren
![]() soll wieder
durch (2.3) definiert sein. Um in der
Basis (2.12) eine eindimensionale
Schrödinger-Gleichung anschreiben zu können, greifen wir auf die
Störungsrechnung zurück.
soll wieder
durch (2.3) definiert sein. Um in der
Basis (2.12) eine eindimensionale
Schrödinger-Gleichung anschreiben zu können, greifen wir auf die
Störungsrechnung zurück.
![]() an.
an.
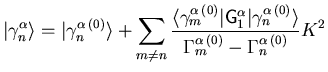
![]() .
.
![]() aus (2.60)
näherungsweise wie folgt angeschrieben.
aus (2.60)
näherungsweise wie folgt angeschrieben.
![]() und
und
![]() .
.
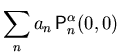
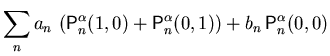
![]() zu berechnen und die eindimensionale Schrödinger-Gleichung
in Matrixform in der Basis der Eigenfunktionen
zu berechnen und die eindimensionale Schrödinger-Gleichung
in Matrixform in der Basis der Eigenfunktionen ![]() anzuschreiben.
anzuschreiben.