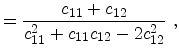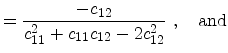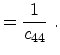3.3 Stress-Strain Relations
A mathematical expression of the stress-strain relation for the elastic
deformation of materials was first suggested by Robert Hooke
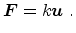 |
(3.10) |
Here,
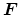 is the applied force,
is the applied force,
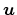 is the deformation of the
elastic body subjected to the force
is the deformation of the
elastic body subjected to the force
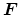 , and
, and 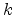 is the material
dependent spring constant. Cauchy generalized Hooke's law for three
dimensional elastic bodies
is the material
dependent spring constant. Cauchy generalized Hooke's law for three
dimensional elastic bodies
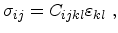 |
(3.11) |
where 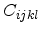 is the elastic stiffness tensor of order four, which contains
81 entries. The number of components can be reduced invoking symmetry
arguments [Kittel96]. For a cubic semiconductor such as Si, Ge or GaAs,
there are only three independent components, namely
is the elastic stiffness tensor of order four, which contains
81 entries. The number of components can be reduced invoking symmetry
arguments [Kittel96]. For a cubic semiconductor such as Si, Ge or GaAs,
there are only three independent components, namely
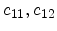 , and
, and
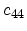 . The elastic stiffness constants for Si and Ge are given in
Table 3.1.
. The elastic stiffness constants for Si and Ge are given in
Table 3.1.
Table 3.1:
Elastic stiffness constants of Si and Ge [Levinshtein99].
| |
Silicon |
Germanium |
Units |
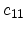 |
166.0 |
126.0 |
GPa |
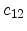 |
64.0 |
44.0 |
GPa |
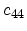 |
79.6 |
67.7 |
GPa |
| |
|
|
|
|
Exploiting the symmetry of a cubic semiconductor the elastic stiffness tensor can be
written as a 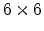 matrix, and generalized Hooke's law reduces to a set of six equations
matrix, and generalized Hooke's law reduces to a set of six equations
 |
(3.12) |
If the stresses are known, the values for the strains are to be determined by
inversion of (3.11). Introducing the elastic compliance tensor
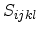 , the inverted equation becomes in the index notation
, the inverted equation becomes in the index notation
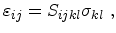 |
(3.13) |
or in matrix form
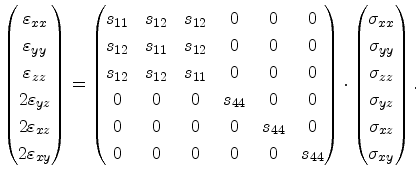 |
(3.14) |
The elastic compliance constants 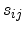 are related to
the elastic stiffness constants
are related to
the elastic stiffness constants 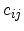 via
via
Note that the stiffness constants are traditionally represented by the symbol 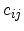 ,
while
,
while 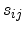 is reserved for the compliance constants.
is reserved for the compliance constants.
Subsections
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
![]() matrix, and generalized Hooke's law reduces to a set of six equations
matrix, and generalized Hooke's law reduces to a set of six equations