![\includegraphics[width=13cm]{figures/SmallLargeSignal.eps}](img528.png)
|
If a device, for example a power RF transistor, has to be characterized under conditions where a harmonic generation takes place, the small-signal approximation has to be replaced by large-signal simulations [241] such as the nonlinear harmonic balance, envelope, or shooting-method simulation [220]. In contrast to small-signal simulation, the device is then not linearized and the harmonic generation as depicted in Figure 2.6 can be taken into account. Rather than ignoring the harmonics and thus getting results which actually violate physical conditions, the additional voltage and current vectors are included in the simulation. Simulators for Harmonic Balance simulations are for example proposed in [206,6,8].
An alternative are Volterra methods which are similar to the small-signal systems besides the fact that they take more than the first term of the Taylor series expansion into account [125].
![\includegraphics[width=13cm]{figures/SmallLargeSignal.eps}](img528.png)
|
Three important parameters for RF and power devices are the power gain and output level, the power added efficiency as the ratio between the difference of the output and input power and the steady-state input power, as well as distortion [241]. These quantities can be efficiently extracted by the Harmonic Balance method.
Harmonic Balance is a highly accurate analysis technique which is also based in the frequency domain [220]. For that reason the large-signal steady-state performance of a semiconductor device can be much faster obtained than using a computationally more expensive transient analysis [177]. Harmonic Balance can be used for simulating analog RF problems which are naturally handled in the frequency domain. Among the results are harmonic distortion, third-order intercept points, gain compression, phase noise, and intermodulation products in non-linear circuits [5]. As the input stimulus is assumed to consist of steady-state sinusoids, the solution of the Harmonic Balance simulation is a sum of steady-state sinusoids including the input frequencies additionally to significant harmonics and mixing terms.
The Harmonic Balance approach consists of an expansion of each device variable, that is
for example ![]() ,
, ![]() , and
, and ![]() , as a Fourier series and solves
for the coefficients
, as a Fourier series and solves
for the coefficients ![]() ,
,
![]() given
as [177]
given
as [177]
![$\displaystyle x_n(t) = X_{n0} + \sum_{h = 1}^{H} \left(X_{n,h}^R \cos(\omega_h(...
...underline{X_{n,h}}} \exp(\ensuremath{\mathrm{j}}\omega_h t) \right) \right] \ ,$](img532.png) |
(2.144) |
The time domain state vector ![]() of length
of length
![]() is given by
[221]
is given by
[221]
| (2.145) |
The input stimulus is usually an either one- or two-tone sinusoid (more than two sinusoids are normally already too expensive) with the form [241]:
| (2.146) |
The benefits of Harmonic Balance are that this approach is able to extract steady-state performance of a device in the presence of potentially longer time constant phenomena, while it avoids excessive number of time steps in multitone analyses [177]. A particular strength of the Harmonic Balance method is that it can include models for linear components which are directly based in the frequency domain. Such models are required for lossy or dispersive transmission lines [125].
For the solution of the resulting equation systems, special algorithms and numerics, such as the restarted version of GMRES, are required [220]. Furthermore, difficulties are reported in case of strongly nonlinear circuits or circuits containing signals with abrupt transitions [125].
Finally it has to be noted that the linearity is an important prerequisite for
advanced systems as higher-order harmonics at the output can be neglected. In
a nonlinear device harmonics are generated even for pure sinusoidal inputs.
An important figure of merit is the so-called third-order inter-modulation
intercept point [171], at which the output amplitude of the third
harmonic equals that of the fundamental one [135]. For that reason,
the third harmonic intercept voltage parameter is considered to give a good
indication of the device linearity. For MOS devices,
![]() can be
approximately obtained from steady-state characteristics [239]
can be
approximately obtained from steady-state characteristics [239]
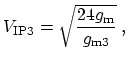 |
(2.147) |
The
![]() approach obviously requires the ability for solving complex-valued
linear equation systems, for which several methods can be applied. One
possibility is to reuse a real-valued assembly and solver system, split the
real and imaginary part as suggested in [127] and solve both systems
separately. If the complex-valued matrix has the form
approach obviously requires the ability for solving complex-valued
linear equation systems, for which several methods can be applied. One
possibility is to reuse a real-valued assembly and solver system, split the
real and imaginary part as suggested in [127] and solve both systems
separately. If the complex-valued matrix has the form
| (2.148) |
![$\displaystyle - \left[ \begin{array}{cc} \ensuremath{\mathbf{J}} & \ensuremath{...
...thbf{b_\mathrm{R}}} \\ \ensuremath{\mathbf{b_\mathrm{I}}} \end{array}\right]\ ,$](img548.png) |
(2.149) |
| (2.150) | |
| (2.151) |
In terms of memory consumption this approach has, especially for three-dimensional simulations, severe disadvantages, since the dimension doubles causing a fourfold-sized system matrix. Thus, the computational effort for factorization can be excessive. In [127] iterative methods like block-Gauss-Seidel or block-SOR are suggested for reducing this effort. In Chapter 4 and Chapter 5, complex-valued assembly and solver systems are discussed. In addition, the results of an evaluation of these approaches is given.