1 Introduction: What is Single Electronics?

It has long been an axiom of mine
that the little things are infinitely the most important.
Sir Arthur Conan Doyle

...I wish to give an account of some investigations which have led to the conclusion that the carriers of negative electricity are bodies, which I have called corpuscles, having a mass very much smaller than that of the atom of any known element, and are of the same character from whatever source the negative electricity may be derived.
Joseph John Thomson from his Nobel Prize Award Address, 1906

We talk about single-electronics  whenever it is possible to control the movement and position of a single or small number of electrons. To understand how a single electron can be controlled, one must understand the movement of electric charge through a conductor. An electric current can flow through the conductor because some electrons are free to move through the lattice of atomic nuclei. The current is determined by the charge transferred through the conductor. Surprisingly this transferred charge can have practically any value, in particular, a fraction of the charge of a single electron. Hence, it is not quantized.

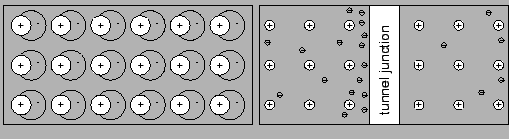
This, at first glance counterintuitive fact, is a consequence of the displacement of the  electron cloud against the lattice of atoms. This shift can be changed continuously and thus the transferred charge is a continuous quantity (see left side of Fig. 1.1).

   

Figure 1.1: The left side shows, that the electron cloud shift against the lattice of atoms is not quantized. The right side shows an accumulation of electrons at a tunnel junction.

$\parbox{20cm}{ \resizebox{0.45\textwidth}{!}{\includegraphics{electr... ...ift.eps}} \resizebox{0.45\textwidth}{!}{\includegraphics{atomic_junction.eps}}}$

If a  tunnel junction interrupts an ordinary conductor,   electric charge will move through the system by both a continuous and discrete process. Since only discrete electrons can tunnel through junctions, charge will accumulate at the surface of the electrode against the isolating layer, until a high enough bias has built up across the tunnel junction (see right side of Fig. 1.1). Then one electron will be transferred. K. Likharev [79] has coined the term  `dripping tap' as an analogy of this process. In other words, if a single tunnel junction is biased with a constant current I, the so called  Coulomb oscillations will appear with  frequency f = I/e, where e is the charge of an electron (see Fig. 1.2).

  

Figure 1.2: Current biased tunnel junction showing Coulomb oscillations.

$\parbox{20cm}{ \includegraphics{current_biased_tj1.eps} \resizebox{2... ...}{\includegraphics{dripping_tap.eps}} \includegraphics{current_biased_tj2.eps}}$

Charge continuously accumulates on the tunnel junction until it is energetically favorable for an electron to tunnel. This discharges the tunnel junction by an elementary charge e. Similar effects are observed in  superconductors. There, charge carriers are  Cooper pairs, and the characteristic frequency becomes f = I/2e, related to the so called  Bloch oscillations.

The current biased  tunnel junction is one very simple circuit, that shows the controlled transfer of electrons. Another one is the  electron-box (see Fig. 1.3).

  

Figure 1.3: The electron-box can be filled with a precise number of electrons.

$\parbox{20cm}{ \includegraphics{electron_box1.eps} \includegraphics{electron_box2.eps}}$

A particle is only on one side connected by a tunnel junction. On this side electrons can tunnel in and out. Imagine for instance a metal particle  embedded in oxide, as shown in Fig. 1.4.

  

Figure 1.4: Metal particle embedded in oxide. Tunneling is only possible through the thin top layer of oxide.

The top oxide layer is thin enough for electrons to tunnel through. To transfer one electron onto the particle, the Coulomb energy E_C = e²/2C, where C is the particles capacitance, is required. Neglecting thermal and other forms of energy, the only energy source available is the bias voltage V_b. As long as the bias voltage is small enough, smaller than a threshold V_th = e/C, no electron can tunnel, because not enough energy is available to charge the island. This behavior is called the Coulomb blockade . Raising the bias voltage will populate the particle with one, then two and so on electrons, leading to a staircase-like characteristic.

It is easily understandable, that these single-electron phenomena, such as Coulomb oscillations and Coulomb blockade, only matter, if the Coulomb energy is bigger than the  thermal energy. Otherwise  thermal fluctuations will disturb the motion of electrons and will wash out the quantization effects. The necessary condition is
$$\begin{gather}E_C = \frac{e^2}{2C} > k_B T, \end{gather}$$
where k_B is Boltzmann's constant and T is the absolute temperature. This means that the capacitance C has to be smaller than 12 aF for the observation of charging effects at the temperature of liquid nitrogen and smaller than 3 aF for charging effects to appear at room temperature. A second condition for the observation of charging effects is, that  quantum fluctuations of the number of electrons on an island must be negligible. Electrons need to be well localized on the islands. If electrons would not be localized on islands one would not observe charging effects, since islands would not be separate particles but rather one big uniform space. The charging of one island with an integer number of the elementary charge would be impossible, because one electron is shared by more than one island. The Coulomb blockade would vanish, since no longer would a lower limit of the charge, an island could be charged with, exist. This leads to the requirement that all tunnel junctions must be opaque enough for electrons in order to confine them on islands. The `transparency' of a tunnel junction is given by its  tunnel resistance R_T which must fulfill the following condition for observing discrete charging effects
$$\begin{gather}R_T > \frac{h}{e^2} \doteq 25813\ \Omega, \end{gather}$$
where h is Planck's constant. This should be understood as an order-of-magnitude measure, rather than an exact threshold.

Therefore, these effects are experimentally verifiable only for very small high-resistance tunnel junctions, meaning small particles with small capacitances and/or very low temperatures. Advanced fabrication techniques, such as the production of granular films with particle sizes down to 1 nm, and deeper physical understanding allow today the study of many charging effects at room temperature [105].

Based on the Coulomb blockade many interesting devices are possible, such as precise current standards [82], very sensitive electrometers [65], logic gates [103] [102], and memories [89] [109] with ultra low power consumption, down-scalability to atomic dimensions, and high speed of operation. Altogether, single-electronics will bring new and novel devices and is a very promising candidate to partly replace MOS technology in the near future.