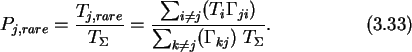Next: 4 Implementation Issues
Up: 3 Simulation of Single
Previous: 3.5 Comparison between Master
3.6 Combination of Monte Carlo Method with Direct Calculation
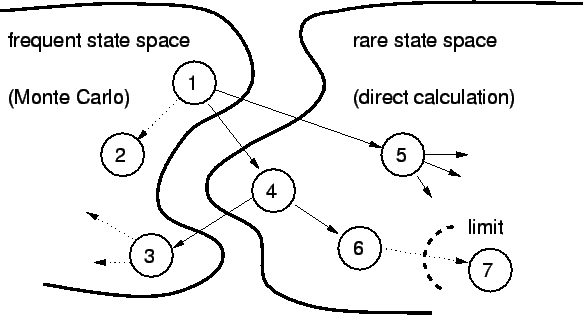
Consider all possible states as divided into two subspaces, the
frequent state
space and the rare state space, as shown in
Fig. 3.9.
Figure 3.9:
Partition of the state space into a frequent and a
rare state domain.
 |
The MC part simulates only the frequent state space, which gives the
occupation probabilities of frequent states. The occupation probability
Pi is calculated as the ratio of time Ti spent in state i to the
total simulation time
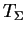 .
.
Pi is the solution to the stationary ME for the frequent states.
Instead of waiting for the MC simulator to step into the rare state space,
which would result in impractically long simulation times, we directly
calculate the contribution of events leading to rare states by stepping
through the event tree (see Fig. 3.10)
starting at frequent states.
Figure 3.10:
Direct calculation of the contribution of rare states and events
by stepping through the event tree. Solid arrows mark transitions that
are considered for the direct calculation part.
 |
The essential assumption is that the rare states cause only a small
perturbation to the frequent state probabilities.

where
Tj,rare is the time spent in the rare state j, which can be
directly calculated from the stationary ME.
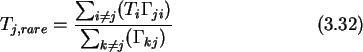
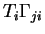 is the number of times the rare state j would
be in average visited from state i,
is the number of times the rare state j would
be in average visited from state i,
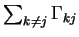 is the
exit rate of state j and thus
is the
exit rate of state j and thus
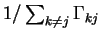 is the average
time spent in state j for one visit. We are using time averages for the
direct calculation. Actually the durations are distributed with a Poisson
distribution. However, the directly calculated rare state space is only a small
perturbation to the frequent state space which is calculated with a MC
method where the Poisson distribution of the tunnel durations is fully
incorporated.
The occupation probability for a rare state is therefore
is the average
time spent in state j for one visit. We are using time averages for the
direct calculation. Actually the durations are distributed with a Poisson
distribution. However, the directly calculated rare state space is only a small
perturbation to the frequent state space which is calculated with a MC
method where the Poisson distribution of the tunnel durations is fully
incorporated.
The occupation probability for a rare state is therefore
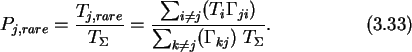
The algorithm follows all possible events starting
at frequent states. If a frequent state is encountered the algorithm
terminates that branch, because the state probability is already known.
Once the
probability of a state is lower than a predefined limit no further descent
into following branches from this state is made (see Fig. 3.10).




Next: 4 Implementation Issues
Up: 3 Simulation of Single
Previous: 3.5 Comparison between Master
Christoph Wasshuber


![]()
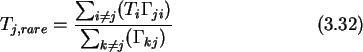
![]() is the number of times the rare state j would
be in average visited from state i,
is the number of times the rare state j would
be in average visited from state i,
![]() is the
exit rate of state j and thus
is the
exit rate of state j and thus
![]() is the average
time spent in state j for one visit. We are using time averages for the
direct calculation. Actually the durations are distributed with a Poisson
distribution. However, the directly calculated rare state space is only a small
perturbation to the frequent state space which is calculated with a MC
method where the Poisson distribution of the tunnel durations is fully
incorporated.
The occupation probability for a rare state is therefore
is the average
time spent in state j for one visit. We are using time averages for the
direct calculation. Actually the durations are distributed with a Poisson
distribution. However, the directly calculated rare state space is only a small
perturbation to the frequent state space which is calculated with a MC
method where the Poisson distribution of the tunnel durations is fully
incorporated.
The occupation probability for a rare state is therefore