H Arnoldi Algorithm

  The Arnoldi algorithm [44] builds an orthonormal basis $\boldsymbol{B_m}=[\boldsymbol{b_1},\boldsymbol{b_2},\ldots,\boldsymbol{b_m}]$ for a Krylov subspace $K_m(\boldsymbol{A},\boldsymbol{b})\equiv \text{span}\{\boldsymbol{b},\boldsymbol{A}\boldsymbol{b},\ldots, \boldsymbol{A}^{m-1}\boldsymbol{b}\}$.

1. Set $\boldsymbol{b_1} = \boldsymbol{b}/\Vert\boldsymbol{b}\Vert _2$ this makes the first vector a unit-vector

2. For $j=1,2,\ldots,m$ do

Compute z=Ab_j next vector spanning the subspace.

For $i=1,2,\dots,j$ do

Compute h_ij=b_i^Tz $\parbox{\textwidth}{compute the projection of new vector $\boldsymbol{z}$\space onto already calculated orthonormal vectors $\boldsymbol{b_i}$ .}$

Compute z=z-h_ijb_i 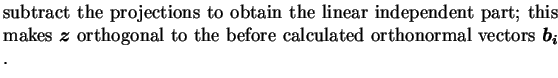$\parbox{\textwidth}{subtract the projections to obtain the linear i... ... orthogonal to the before calculated orthonormal vectors $\boldsymbol{b_i}$ .}$

Compute $h_{j+1,j}=\Vert\boldsymbol{z}\Vert _2$ and b_j+1=z/h_j+1,j make b_j+1 a unit vector.

The computed basis B_m is orthonormal and the $m\times m$ upper Hessenberg matrix H_m, formed by the coefficients h_ij satisfies the relationship
$$\begin{gather}\boldsymbol{AB_m}=\boldsymbol{B_mH_m}+h_{m+1,m}\boldsymbol{b_{m+1}e_m}^T. \end{gather}$$