



Next: H Arnoldi Algorithm
Up: Dissertation Christoph Wasshuber
Previous: F Second Order Co
G Rational Padé Approximations
The (p,q) Padé approximant to the matrix exponential
eX is,
by definition, the unique (p,q) rational function [100]
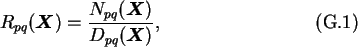
which matches the Taylor series expansion of
eX through terms
to the power p+q. Its coefficients are therefore determined by solving the
algebraic equations
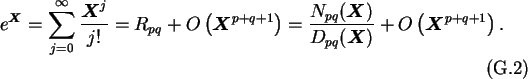
The result is
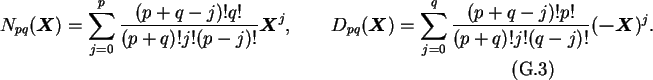
Choosing p=q one obtains the diagonal Padé approximation. This choice
is to prefer, because it yields a higher order approximation with the same
amount of computation.
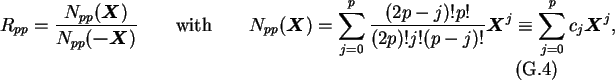
where the coefficients cj can be conveniently constructed by means of the
recursion
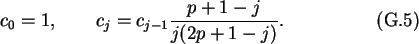
The computation of the polynomials are best done with a Horner scheme. C. Moler
and C. Van Loan [87] showed that if
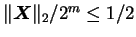 ,
then
,
then
![\begin{gather}\left[R_{pp}\left(\frac{\boldsymbol{X}}{2^m}\right)\right]^{2^m}=e...
...^{2p-3}\frac{(p!)^2}{(2p)!(2p+1)!}\approx
0.34\cdot 10^{-15} (p=6)
\end{gather}](img460.gif)
Christoph Wasshuber
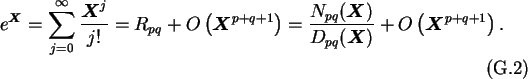
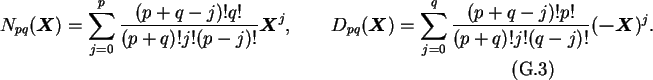
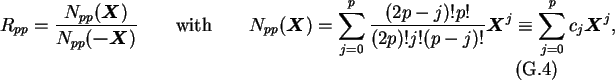
![\begin{gather}\left[R_{pp}\left(\frac{\boldsymbol{X}}{2^m}\right)\right]^{2^m}=e...
...^{2p-3}\frac{(p!)^2}{(2p)!(2p+1)!}\approx
0.34\cdot 10^{-15} (p=6)
\end{gather}](img460.gif)