A.2 PCA of a Tetrahedron

In the following I want to show how the afore said works in detail applied to a tetrahedron.

**Figure A.1:** System of four points form a tetrahedron.
$\includegraphics[width=0.23\textwidth]{pics/one-tet.eps}$

Figure A.1 shows an arbitrary constellation of four points $P_1,\ldots,P_4$ which form a tetrahedron. In the following a step by step recipe is given for applying PCA to this constellation.

Collecting Data

First three sets are formed, namely $\mathbf{x}$ , $\mathbf{y}$ , and $\mathbf{z}$ , by collecting the coordinates of the four tetrahedron points $P_1,\ldots,P_4$ :

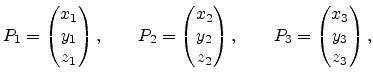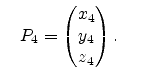$\displaystyle P_1 = \begin{pmatrix}x_1 \ y_1 \ z_1 \end{pmatrix}, \qquad P_2 ... ...z_2 \end{pmatrix}, \qquad P_3 = \begin{pmatrix}x_3 \ y_3 \ z_3 \end{pmatrix},$ and $\displaystyle \quad P_4 = \begin{pmatrix}x_4 \ y_4 \ z_4 \end{pmatrix}. \qquad$

(A.12)

$\displaystyle \mathbf{x}=\{x_1, x_3, x_3, x_4\}, \qquad \mathbf{y}=\{y_1, y_3, y_3, y_4\},$ and $\displaystyle \quad \mathbf{z}=\{z_1, z_3, z_3, z_4\}.$

(A.13)

Subtract the Mean

For PCA the next step is to subtract the mean from each data set, so three new sets are defined:

$\begin{displaymath}\begin{array}{lclclclcll } \displaystyle \mathbf{x}'&= \{& x_... ...\;& z_3-\mu_\mathbf{z},&\;& z_4-\mu_\mathbf{z} &\}. \end{array}\end{displaymath}$

(A.14)

Note that the mean value of the three data sets $\mathbf{x}'$ , $\mathbf{y}'$ , and $\mathbf{z}'$ presented in Equation (A.14) is equal to zero, i.e. $\mu_{\mathbf{x}'} = \mu_{\mathbf{y}'} = \mu_{\mathbf{z}' = 0}$ .

Calculate the Covariance Matrix

With respect to Equation (A.8) a $3 \times 3$ covariance matrix is formed from the three mean adjusted data sets $\mathbf{x}'$ , $\mathbf{y}'$ , and $\mathbf{z}'$ , see Equation (A.14).

$\displaystyle C^{3 \times 3} := \begin{pmatrix}\operatorname{cov}(\mathbf{x}',\... ...f{z}',\mathbf{y}') & \operatorname{cov}(\mathbf{z}',\mathbf{z}') \end{pmatrix}.$

(A.15)

Under the assumption that Equation (A.11) holds, there exist exact three real eigenvalues $\lambda_1$ , $\lambda_2$ , and $\lambda_3$ (since the covariance matrix is symmetric) and three corresponding orthogonal eigenvectors $\vec{x}_1$ , $\vec{x}_2$ , and $\vec{x}_3$ . If the three eigenvalues are not different, the corresponding eigenvectors cannot be determined uniquely. In this case an arbitrary system of three orthogonal vectors is used for a so-called ellipsoidal glyph visualization.