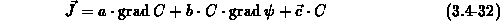
In the general case, when both diffusive and convective components exist (3.4-32), we use a discretization scheme which is similar to the approach of Scharfetter and Gummel [Sch69] applied in device simulation. Hence, we will sketch its derivation just briefly.
Following Scharfetter and Gummel we integrate the ODE (3.4-35),
assuming that the coefficients 
, 
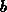and 
, the electric field
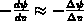, and the flux 
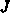are constant in the integration interval 
.
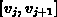We define the cell Reynolds number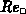 
(3.4-36) using 
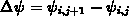, the potential difference, and the grid spacing 
.
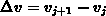In Scharfetter's case the cell Reynolds number was 
, the ratio of the voltage difference
between grid points to the thermal voltage. Solving (3.4-35)
and matching to the boundary conditions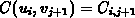 
and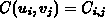 
, we obtain (3.4-37). 
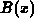is the Bernoulli function (3.4-38).
It is well known that the application of a standard central difference approximation to the flux density would give rise to oscillations if the cell Reynolds number exceeds 2.0 [Bür90].
In the expressions for the fluxes (3.4-33), (3.4-34) we
split the velocity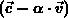 
into components in
- and 
-direction. Therefore, we use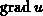 
and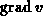 
as
projectors, respectively. With this velocity component as value for the
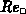cell Reynolds number (3.4-36) and the
approximation (3.4-37) we discretize the fluxes
(3.4-33) and (3.4-34).
