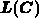 , and
, and 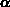 a coefficient matrix with at least
one non-vanishing eigenvalue.
a coefficient matrix with at least
one non-vanishing eigenvalue. 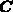 denotes the vector of dependent
values.
denotes the vector of dependent
values.




We return to our system of parabolic differential equations
(3.3-61) - (3.3-63) in the form (3.4-42),
where the spatial derivatives are compactly written using the elliptic
operator 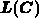 , and
, and 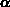 a coefficient matrix with at least
one non-vanishing eigenvalue.
a coefficient matrix with at least
one non-vanishing eigenvalue. 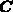 denotes the vector of dependent
values.
denotes the vector of dependent
values.
In order to obtain a finite difference replacement of (3.4-42), the domain (in space and time) to be examined is covered by a grid in space and time, or expressed differently, the domain is covered by space grids at different time levels. In multi level schemes (see e.g. [Gea71], [Mit80]) the concentration values at multiple past time levels are required, preferably on identical space grids, to calculate the concentrations at the present. Due to space grid adaption the concentrations at past time steps ought to be interpolated to the adapted grid, which would disturb time discretization. Therefore we restrict ourselves to two level schemes involving two adjacent time levels.
We have already given discretization formulae for the space derivatives (elliptic operator) at one time level. Difference formulae involving two adjacent time levels are obtained from Taylor expansion (3.4-43).
Out of the numerous methods in common use for approximating (3.4-42), see for instance [Mit80] and [Vem81]), there is no universal best method. However, the approximating difference formula must pass a stability test.
To simplify the discussion of some basic properties of the discretization schemes, the dependent variables are discretized with respect to time and are left continuous in space. The simplest scheme is to use a forward difference approximation for the time derivatives (3.4-44).
The computational stencil for this scheme is shown in
Figure 3.4-5 (left). Here, the unknown value at
one grid point is expressed in terms of known values at other grid points; such formulae are called explicit methods. The
stability analysis by the Fourier series method, introduced by John von
Neumann, gives a sufficient condition for the time step size. For the case
of pure diffusive fluxes (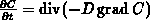 discretized on an equidistant grid (
discretized on an equidistant grid (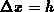 ,
, 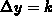 ) the stability condition restricts the time step
to (3.4-45) [Vem81].
) the stability condition restricts the time step
to (3.4-45) [Vem81].
This condition interpreted physically means that the maximum permissible time step is just half the diffusion time associated with the width of the rectangular grid cell, or rather the time for the information to travel from the cell center to the nearest cell boundary.
This severe restriction on the time step is not feasible in practice, therefore we refrain from using fully explicit methods.
We get the backward Euler scheme, a fully implicit method, if we use a backward difference approximation for the time derivative (3.4-46).
The computational stencil for this scheme is shown in Figure 3.4-5 (right). This method is unconditionally stable for any time step size [Vem81].
According to the backward differences formula (BDF1) (3.4-46), we discretize the time derivatives in the computational domain by (3.4-47).



