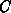 ) at a time
) at a time 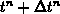 , given their values at
time
, given their values at
time 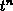 , where
, where 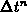 is a sufficiently small time step.
is a sufficiently small time step.




With the solution algorithm for the system of nonlinear algebraic equations
we are able to calculate the values of the dependent variables
(concentrations 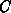 ) at a time
) at a time 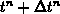 , given their values at
time
, given their values at
time 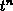 , where
, where 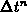 is a sufficiently small time step.
is a sufficiently small time step.
Here we give an overview of the implemented algorithm for the simulation of a complete transient process, i.e. the algorithm for calculating the concentrations at a desired end time, given the initial concentrations. We describe the implemented algorithm for the most general case which includes moving boundaries. In Section 3.6.1 and Section 3.6.2 we explain the time step control and the adaption of the spatial grid, respectively.
The schematic program flow for the time integration is shown in Program 3.6-1.
In the initialization phase all necessary information is read from a PIF input file (Profile Interchange Format [Fas91]). Usually, we read the initial dopant profiles, the process parameters and information about the physical models and the geometry information. For moving boundary problems we build a list of geometry snapshots sorted by the corresponding simulation time. An example for the geometry specification is given in Program 3.6-2.
Later on, this list is used to determine the geometric shape at a
specific time 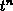 . An initial time step
. An initial time step 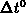 is estimated from the
initial solution
is estimated from the
initial solution 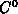 and the physical model as explained in
Section 3.6.1 unless
and the physical model as explained in
Section 3.6.1 unless 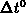 has been provided by the user.
has been provided by the user.
For each time step in the time integration loop we first update the geometry and the metric coefficients. Then we solve the nonlinear system by a Newton algorithm as described in the previous section. If the Newton algorithm did not converge we retry the solution with half time step size. If the Newton algorithm did converge but the desired accuracy of the time discretization is not reached a smaller time step is estimated as described in Section 3.6.1 and we retry the solution with the smaller time step size.
For a sufficient time step, i.e. if the desired accuracy was reached, we
check and update the computational grid (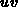 -phys) for the two
relevant geometries (
-phys) for the two
relevant geometries (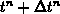 ,
, 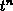 ) by interpolation. If new grid
points were inserted we solve the nonlinear system once more on the new grid
to guarantee a self-consistent solution. The time step size
) by interpolation. If new grid
points were inserted we solve the nonlinear system once more on the new grid
to guarantee a self-consistent solution. The time step size 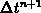 for the next time step is estimated from the accuracy of the actual time step.
for the next time step is estimated from the accuracy of the actual time step.



