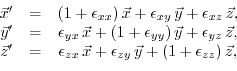 |
(3.1) |
Assuming a uniform deformation, a point located at
![]() will be shifted to
will be shifted to
![]() , which leads to the displacement
, which leads to the displacement ![]() defined as
defined as
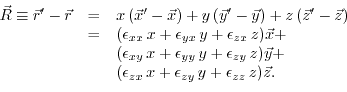 |
(3.2) |
Further generalization leads to a description for non-uniform deformation, introducing a position dependent vector function
![]() ,
,
| (3.3) |
Restricting to small displacements from ![]() , the displacement function
, the displacement function
![]() can be developed into a Taylor series and truncated after the linear term at
can be developed into a Taylor series and truncated after the linear term at
![]() , leading to a relation between the local displacement tensor and the displacement function,
, leading to a relation between the local displacement tensor and the displacement function,
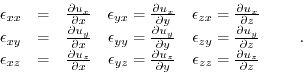 |
Therefore, the displacement can be expressed as
![]() .
Frequently, the displacements
.
Frequently, the displacements
![]() are expressed via the strain tensor
are expressed via the strain tensor
![]() to describe the deformation of a body in three dimensions. In the limit of small deformations, the strain tensor is known as the Green tensor or Cauchy's infinitesimal strain tensor,
to describe the deformation of a body in three dimensions. In the limit of small deformations, the strain tensor is known as the Green tensor or Cauchy's infinitesimal strain tensor,
| (3.4) |
The relative length change in the
![]() direction is described by the diagonal coefficients
direction is described by the diagonal coefficients
![]() , while the off-diagonal elements
, while the off-diagonal elements
![]() denote the angular distortions by shear strains.
denote the angular distortions by shear strains.
Also very common are the engineering strains ![]() , which are linked with the strain tensor as follows:
, which are linked with the strain tensor as follows:
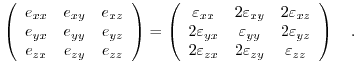 |
(3.5) |
| (3.6) |