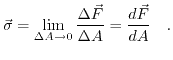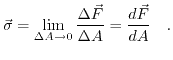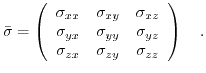3.2 Stress

In mechanical equilibrium, all forces acting on a body must sum up to zero. In a more general and sophisticated formulation, within a body forces which an enclosed volume imposes on the remainder of the body, must be in equilibrium with the forces upon it from the remainder of the body. Cauchy was the first that formulated this principle and enabled a way to calculate stress. Considering a small element of the body enclosed by the area 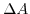$\Delta A$ and looking at the forces 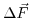$\Delta \vec{F}$, which act on this element, the stress at this point can be determined. The stress vector 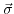$\vec{\sigma}$ is then defined as the limit of the following expression for an infinitesimal small area:

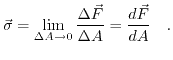$$\vec{\sigma} = \lim_{\Delta A \rightarrow 0} \frac{\Delta \vec{F}}{\Delta A}=\frac{d\vec{F}}{dA}\quad.$$ (3.7)

Therefore, for a given plane the stress vector can be decomposed in a force perpendicular to the plane and two orthogonal in-plane vectors. The force normal to the surface is called normal component and the forces that act in-plane are the shear components. These three forces in combination with the three main planes ( 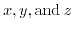$x, y, \mathrm{and}\: z$) form the nine components of the stress tensor Fig. 3.1:

Figure 3.1: Scheme of stress components and how they act on an infinitesimal cube.

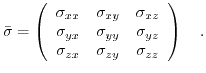$$\bar{\sigma}=\left(\begin{array}{ccc} \sigma_{xx}&\sigma_{xy}&\si... ...{yy}&\sigma_{yz}\\ \sigma_{zx}&\sigma_{zy}&\sigma_{zz} \end{array}\right)\quad.$$ (3.8)

Due to the moment equilibrium for every plane, the shear stress components across the diagonal are identical

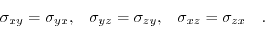$$\begin{array}{ccc}\sigma_{xy}=\sigma_{yx}, & \sigma_{yz}=\sigma_{zy}, & \sigma_{xz}=\sigma_{zx}\quad.\end{array}$$ (3.9)