



Next: 3.5 Strain and Bulk
Up: 3. Strain and Semiconductor
Previous: 3.3 Stress-Strain Relation
The position of a crystal plane is determined by three independent non-collinear points. If these points reside on independent crystal axes, the plane can be characterized in units of the axes. However, it is more convenient to describe the planes location via Miller indices [164,162]. The Miller indices are a triplet of integer values 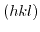 , which denote the ratio between the points that intercept the plane and the chosen crystal axes. The Miller indices can be found as follows:
, which denote the ratio between the points that intercept the plane and the chosen crystal axes. The Miller indices can be found as follows:
- Define three lattice vectors
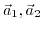 , and
, and
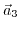 . In the case of a cubic crystal, the lattice vectors are chosen along the edges of the crystallographic unit cell (unit cube).
. In the case of a cubic crystal, the lattice vectors are chosen along the edges of the crystallographic unit cell (unit cube).
- Identify the intercepting points
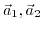 , and
, and
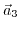 between the plane and the lattice vectors, and express them in units of the lattice vectors
between the plane and the lattice vectors, and express them in units of the lattice vectors
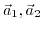 , and
, and
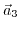 .
.
- Calculate the reciprocal of the
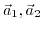 , and
, and
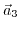 and choose the smallest three integer values
and choose the smallest three integer values 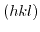 that have a greatest common divisor of one.
that have a greatest common divisor of one.
Negative indices are denoted by a bar above their value 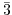 or
or 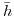 . If there is no interception between an axis and the plane, the Miller index is 0 (they intercept in infinity).
Depending on the brackets used, their meaning can be further distinguished:
. If there is no interception between an axis and the plane, the Miller index is 0 (they intercept in infinity).
Depending on the brackets used, their meaning can be further distinguished:
-
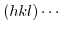 round brackets denote a certain plane or the vector perpendicular to the plane
round brackets denote a certain plane or the vector perpendicular to the plane
-
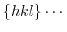 curly braces stand for all planes that are equivalent to
curly braces stand for all planes that are equivalent to 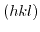 due to the symmetry of the crystal.
due to the symmetry of the crystal.
-
![$ \left[hkl\right]\cdots$](img375.png) these brackets mean a given direction in the crystall.
these brackets mean a given direction in the crystall.
-
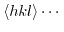 angle brackets describe all directions that are equivalent to the direction
angle brackets describe all directions that are equivalent to the direction
![$ \left[hkl\right]$](img377.png) .
.
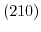 means that the plane intersects the axis vectors at
means that the plane intersects the axis vectors at
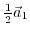 and at
and at
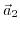 . Additionally, the direction vector
. Additionally, the direction vector
![$ \left[hkl\right]$](img377.png) is always perpendicular to the plane
is always perpendicular to the plane
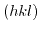 , for cubic crystal structures.
, for cubic crystal structures.




Next: 3.5 Strain and Bulk
Up: 3. Strain and Semiconductor
Previous: 3.3 Stress-Strain Relation
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors
![]() or
or ![]() . If there is no interception between an axis and the plane, the Miller index is 0 (they intercept in infinity).
Depending on the brackets used, their meaning can be further distinguished:
. If there is no interception between an axis and the plane, the Miller index is 0 (they intercept in infinity).
Depending on the brackets used, their meaning can be further distinguished:
![]() means that the plane intersects the axis vectors at
means that the plane intersects the axis vectors at
![]() and at
and at
![]() . Additionally, the direction vector
. Additionally, the direction vector
![]() is always perpendicular to the plane
is always perpendicular to the plane
![]() , for cubic crystal structures.
, for cubic crystal structures.